
【题目】乘法公式的探究及应用.
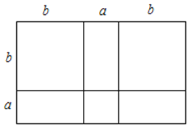
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积.
方法1:______;方法2:______.
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.______;
(3)类似的,请你用图1中的三种纸片拼一个图形验证:
(a+b)(a+2b)=a2+3ab+2b2
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(x-2016)2+(x-2018)2=34,求(x-2017)2的值.

【答案】(1) (a+b)2;a2+b2+2ab;(2)(a+b)2=a2+2ab+b2;(3)见解析;(4)①7;②16.
【解析】
(1)第一种方法:直接用正方形的面积公式求解;第二种方法将其看做是一个两个正方形和两个长方形,分别求出面积再求和即可.
(2)依据(1)中的代数式,即可得到所求的关系;
(3)画出长为a+2b,宽为a+b的长方形,即可完成验证;
(4)①依据a+b=5,可得(a+b)2=25,进而得出a2+b2+2ab=25,再将a2+b2=11,即可得到ab=7;②设x-2017=a,则x-2016=a+1,x-2018=a-1,依据(x-2016)2+(x-2018)2=34,即可得到∴(a+1)2+(a-1)2=34,然后化简得a2=16,即可完成解答.
解:(1)图2大正方形的面积=(a+b)2;图2大正方形的面积=a2+b2+2ab;
故答案为:(a+b)2;a2+b2+2ab;
(2)由题可得(a+b)2,a2+b2,ab之间的等量关系为:(a+b)2=a2+2ab+b2;
故答案为:(a+b)2=a2+2ab+b2;
(3)如图所示,
(4)①∵a+b=5,
∴(a+b)2=25,即a2+b2+2ab=25,
又∵a2+b2=11,
∴ab=7;
②设x-2017=a,则x-2016=a+1,x-2018=a-1,
∵(x-2016)2+(x-2018)2=34,
∴(a+1)2+(a-1)2=34,
∴a2+2a+1+a2-2a+1=34,
∴2a2+2=34,
∴2a2=32,
∴a2=16,
即(x-2017)2=16.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
售价(元/盏) | 60 | 100 |
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,⊙O过AC的中点D,DE⊥BC,交BC于点E.
(1)求证:DE是⊙O的切线;
(2)如果CD=8,CE=6,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
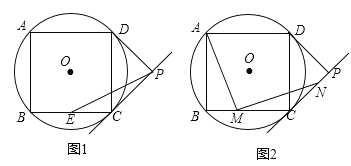
【题目】如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.
(1)如图1,求⊙O的半径;
(2)如图1,若点E是BC的中点,连接PE,求PE的长度;
(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.

(1)求证:CD为⊙O的切线;
(2)若CD=2AD,⊙O的直径为10,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列方程的特征及其解的特点.
①x+![]() =-3的解为x1=-1,x2=-2;
=-3的解为x1=-1,x2=-2;
②x+![]() =-5的解为x1=-2,x2=-3;
=-5的解为x1=-2,x2=-3;
③x+![]() =-7的解为x1=-3,x2=-4.
=-7的解为x1=-3,x2=-4.
解答下列问题:
(1)请你写出一个符合上述特征的方程为________,其解为________;
(2)根据这类方程的特征,写出第n个方程为________,其解为________;
(3)请利用(2)的结论,求关于x的方程x+![]() =-2(n+2)(其中n为正整数)的解.
=-2(n+2)(其中n为正整数)的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(3,1),则点A2018的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )

A.30°B.35°C.40°D.45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com