
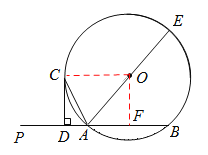
【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.

(1)求证:CD为⊙O的切线;
(2)若CD=2AD,⊙O的直径为10,求线段AB的长.
【答案】(1)见解析(2)![]()
【解析】
试题(1)要证CD为⊙O的切线,只要证CD垂直于对切点的半径,故作辅助线:连接OC,由三角形三个内角和为180°的性质和等腰三角形的判定和性质,即能证出∠DCO =90°,从而得证;
(2)要求AB的长,就要考虑它是三角形中的线段或与三角形中的线段有关系,根据垂径定理,只要作OF⊥AB,即有AB=2AF,故只要求出AF即可,由勾股定理和等量代换即可求得.
试题解析:(1)如图,连接OC,
∵点C在⊙O上,OA=OC,∴∠OCA=∠OAC.
∵CD⊥PA,∴∠CDA=90°.∴∠CAD+∠DCA=90°.
∵AC平分∠PAE,∴∠DAC=∠CAO.
∴∠DCO=∠DCA+∠ACO=∠DCA+∠CAO=∠DCA+∠DAC="90°."
又∵点C在⊙O上,OC为⊙O的半径,∴CD为⊙O的切线.
(2)如图,过O作OF⊥AB,垂足为F,∴∠OCA=∠CDA=∠OFD=90°.
∴四边形OCDF为矩形,∴OC=FD,OF=CD.
∵CD=2AD,设AD=x,则OF=CD=2x,
∵⊙O的直径为10,∴DF=OC=5,∴AF=5-x.
在Rt△AOF中,由勾股定理得![]() .
.
即![]() ,化简得:
,化简得:![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
∴AD="2," AF=5-2=3.
∵OF⊥AB,由垂径定理知,F为AB的中点,∴AB=2AF=6.


科目:初中数学 来源: 题型:
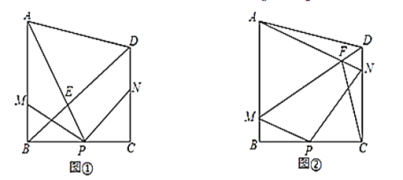
【题目】如图,在四边形![]() 中,
中,![]() 点
点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速移动,点
匀速移动,点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速移动,点
匀速移动,点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速移动.点
匀速移动.点![]() 同时出发,当其中一个点到达终点时,其他两个点也随之停止运动,设移动时间为
同时出发,当其中一个点到达终点时,其他两个点也随之停止运动,设移动时间为![]() .
.
(1)如图①,
①当![]() 为何值时,点
为何值时,点![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?并求出相应的
全等?并求出相应的![]() 的值;
的值;
②连接![]() 交于点
交于点![]() ,当
,当![]() 时,求出
时,求出![]() 的值;
的值;
(2)如图②,连接![]() 交于点
交于点![]() .当
.当![]() 时,证明:
时,证明:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
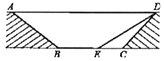
【题目】为缓解交通拥堵,遵义市某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行),通道水平宽度BC为8米,∠BCD=135°,通道斜面CD 的长为6米,通道斜面AB的坡度i=1:![]()
(1)求通道斜面AB的长为多少米;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面CD的坡度变缓,修改后的通道斜面DE的坡角为30°,求此时BE的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=![]() ,tanB=
,tanB=![]() .半径为2的⊙C, 分别交AC、BC于点D、E,得到
.半径为2的⊙C, 分别交AC、BC于点D、E,得到![]() .
.
(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积.
方法1:______;方法2:______.
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.______;
(3)类似的,请你用图1中的三种纸片拼一个图形验证:
(a+b)(a+2b)=a2+3ab+2b2
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(x-2016)2+(x-2018)2=34,求(x-2017)2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外阅读是提高学生素养的重要途径,某校为了了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间(t小时),根据t的长短分为A,B,C,D四类.下面是根据所抽查的人数绘制的两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:

(1)求表格中的a值,并在图中补全条形统计图;
(2)该校现有1300名学生,请你估计该校共有多少学生课外阅读时间不少于1小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O为直线AB上一点,OC平分∠AOE,∠DOE=90°,则以下结论正确的有____________.(只填序号)
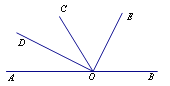
①∠AOD与∠BOE互为余角;
②OD平分∠COA;
③∠BOE=56°40′,则∠COE=61°40′;
④∠BOE=2∠COD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=k1x+b(k1≠0)的图象分别与x轴,y轴相交于点A,B,与反比例函数y2=![]() 的图象相交于点C(﹣4,﹣2),D(2,4).
的图象相交于点C(﹣4,﹣2),D(2,4).
(1)求一次函数和反比例函数的表达式;
(2)当x为何值时,y1>0;
(3)当x为何值时,y1<y2,请直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中每个小正方形边长都是1.
(1)画出△ABC关于直线1对称的图形△A1BlCl;
(2)在直线l上找一点P,使PB=PC;(要求在直线1上标出点P的位置)
(3)连接PA、PC,计算四边形PABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com