
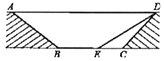
����Ŀ��Ϊ���⽻ͨӵ�£�������ij����ƻ���һ����ͨ������ͨ��һ���ֵĽ�����ͼ��ʾ��ͼ�е���AD��ͨ��BCƽ�У���ͨ��ˮƽ����BCΪ8�ף���BCD=135�㣬ͨ��б��CD �ij�Ϊ6�ף�ͨ��б��AB���¶�i=1��![]()
��1����ͨ��б��AB�ij�Ϊ�����ף�
��2��Ϊ�����������ߵ����ʶȣ��⽫���ͼ�е�ͨ��б��CD���¶ȱ仺���ĺ��ͨ��б��DE���½�Ϊ30�㣬���ʱBE�ij���������������ţ�
���𰸡�(1) 3![]() �ף�(2) ��8+3
�ף�(2) ��8+3![]() ��3
��3![]() ����.
����.
��������
��1������A��AN��CB�ڵ�N������D��DM��BC�ڵ�M��������֪�ó�DM=CM=![]() CD=3
CD=3![]() ����AN=DM=3
����AN=DM=3![]() ���ٽ�Rt��ANB����ͨ��б��AB���¶�i=1��
���ٽ�Rt��ANB����ͨ��б��AB���¶�i=1��![]() ���ó�BN=
���ó�BN=![]() AN=6��Ȼ����ݹ��ɶ������AB��
AN=6��Ȼ����ݹ��ɶ������AB��
��2���Ƚ�Rt��MED�����EM=![]() DM=3
DM=3![]() ���ó�EC=EM-CM=3
���ó�EC=EM-CM=3![]() -3
-3![]() ���ٸ���BE=BC-EC������⣮
���ٸ���BE=BC-EC������⣮
��1������A��AN��CB�ڵ�N������D��DM��BC�ڵ�M��
�ߡ�BCD=135�㣬
���DCM=45�㣬
����Rt��CMD�У���CMD=90�㣬CD=6��
��DM= CM= ![]() CD=3
CD=3![]() ��
��
��AN=DM=3 ![]() ��
��
��ͨ��б��AB���¶�i=1��![]() ��
��
��tan��ABN=![]() ��
��
��BN=![]() AN=6��
AN=6��
��AB=![]() =3
=3![]() ��
��
��ͨ��б��AB�ij�ԼΪ3![]() �ף�
�ף�
��2������Rt��MED�У���EMD=90�㣬��DEM=30�㣬DM=3![]() ��
��
��EM=![]() DM=3
DM=3![]() ��
��
��EC=EM��CM=3![]() ��3
��3![]() ��
��
��BE=BC��EC=8����3![]() ��3
��3![]() ��=8+3
��=8+3![]() ��3
��3![]() ��
��
����ʱBE�ij�ԼΪ��8+3![]() ��3
��3![]() ����.
����.


 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����CD�С�O�ڵ�D��AC��CD����O�ڵ�E������BAC��60�㣬AB��4������Ӱ���ֵ�����ǣ���

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y��![]() (k��0)��ͼ����B(3��2)����B���C����ԭ��O�Գƣ�BA��x���ڵ�A��CD��x���ڵ�D.
(k��0)��ͼ����B(3��2)����B���C����ԭ��O�Գƣ�BA��x���ڵ�A��CD��x���ڵ�D.
��1����������Ⱥ����ı���ʽ��
��2������ACD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶�AB=4��CΪ�߶�AB�ϵ�һ�����㣬��AC��BCΪ�����ȱߡ�ACD�͵ȱߡ�BCE����O����ڡ�CDE�����O�뾶����СֵΪ��������

A. 4 B. ![]() C.
C. ![]() D. 2
D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB����O��ֱ������O��AC���е�D��DE��BC����BC�ڵ�E��
��1����֤��DE����O�����ߣ�
��2�����CD=8��CE=6������O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪kΪʵ��������x��һԪ���η��̣�k+3��x-2��k+2��x+k=0����������ȵ�ʵ���������жϹ���x�ķ��̣�k-1��x-��2k+1��x+k=0 �ĸ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�Ϊ4x��3����Ϊ3x��5�ij�����ֽƬ�м�ȥ�����߳��ֱ�Ϊ2x��1��x��2�������Σ�����Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��PA����O��A��B���㣬AE�ǡ�O��ֱ��,��CΪ��O��һ�㣬��ACƽ�֡�PAE����C��CD��PA������ΪD.

��1����֤��CDΪ��O�����ߣ�
��2����CD=2AD����O��ֱ��Ϊ10�����߶�AB�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽��
��ͼ��������y=![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C������AC��BC����P�ǵ����������������ϵ�һ�����㣬��P�ĺ�����Ϊm������P��PM��x�ᣬ����Ϊ��M��PM��BC�ڵ�Q������P��PE��AC��x���ڵ�E����BC�ڵ�F��
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C������AC��BC����P�ǵ����������������ϵ�һ�����㣬��P�ĺ�����Ϊm������P��PM��x�ᣬ����Ϊ��M��PM��BC�ڵ�Q������P��PE��AC��x���ڵ�E����BC�ڵ�F��
��1����A��B��C��������ꣻ
��2����̽���ڵ�P�˶��Ĺ����У��Ƿ���������ĵ�Q��ʹ����A��C��QΪ������������ǵ��������Σ������ڣ���ֱ��д����ʱ��Q�����ꣻ�������ڣ���˵�����ɣ�
��3�����ú�m�Ĵ���ʽ��ʾ�߶�QF�ij��������mΪ��ֵʱQF�����ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com