
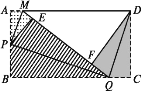
【题目】如图,矩形纸片ABCD,P是AB的中点,Q是BC上一动点,△BPQ沿PQ折叠,点B落在点E处,延长QE交AD于M点,连接PM.
(1)求证:△PAM≌△PEM;
(2)当DQ⊥PQ时,将△CQD沿DQ折叠,点C落在线段EQ上点F处.
①求证:△PAM∽△DCQ;
②如果AM=1,sin∠DMF=![]() ,求AB的长.
,求AB的长.
【答案】(1)见解析;(2)①见解析,②6
【解析】
(1)由矩形的性质及折叠的性质可得PE=PB,∠PEM=∠B=90°,由P点为AB中点可得PA=PB=PE,因为有公共边PM,所以利用HL即可证明△PAM≌△PEM;(2)①由(1)可得∠APM=∠EPM,根据折叠性质可得∠EPQ=∠BPQ,由∠B=90°,DQ⊥PQ可得∠BPQ+∠PQB=90°,∠PQB+∠DQC=180°-∠PQD=90°.进而可证明∠AMP=∠DQC,即可证明△PAM∽△DCQ;②设AP=x,则BP=AP=EP=x,AB=DC=2x,根据△AMP∽△BPQ可得BQ=x2,根据△AMP∽△CQD得CQ=2,进而可得AD=x2+2,根据sin∠DMF=![]() 列方程即可求出x的值,根据AB=2AP即可得答案.
列方程即可求出x的值,根据AB=2AP即可得答案.
(1)∵四边形ABCD是矩形,
∴∠A=∠B=90°,根据折叠的性质可知:PE=PB,∠PEM=∠B=90°;
∵P点为AB中点,
∴PA=PB=PE.
又∵PM=PM,
∴△PAM≌△PEM.
(2)①由(1)知△PAM≌△PEM,
∴∠APM=∠EPM.
根据折叠的性质可知:∠EPQ=∠BPQ,
∴∠APM+∠BPQ=∠EPM+∠EPQ=90°,
∵∠APM+∠AMP=90°,
∴∠BPQ=∠AMP,
∵∠B=90°,DQ⊥PQ,
∴∠BPQ+∠PQB=90°,∠PQB+∠DQC=180°-∠PQD=90°.
∴∠BPQ=∠DQC,
∴∠AMP=∠DQC.
又∵∠A=∠C=90°,
∴△AMP∽△CQD.
②设AP=x,则BP=AP=EP=x,AB=DC=2x,
∵由①知∠BPQ=∠AMP,∠A=∠B=90°,
∴△AMP∽△BPQ.
∴![]() ,即BQ=x2.
,即BQ=x2.
由△AMP∽△CQD得:![]() ,即CQ=2.
,即CQ=2.
AD=BC=BQ+CQ=x2+2.
∵在Rt△FDM中,sin∠DMF=![]() ,DF=DC=2x,
,DF=DC=2x,
∴![]() ,
,
变形得:3x2-10x+3=0,
解方程得:x1=3,x2=![]() (不合题意,舍去)
(不合题意,舍去)
∴AB=2x=6.


科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于港口A的北偏东60°方向,距离港口20海里的B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发,经过20分钟到达C处,求救援船的航行速度.(sin37°≈0.6,cos37°≈0.8,![]() ≈1.732,结果取整数)
≈1.732,结果取整数)
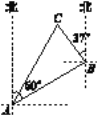
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=mx2﹣2mx+n 的图象经过(0,﹣3).
(1)n= _____________;
(2) 若二次函数 y=mx2﹣2mx+n 的图象与 x 轴有且只有一个交点,求 m 值;
(3) 若二次函数 y=mx2﹣2mx+n 的图象与平行于 x 轴的直线 y=5 的一个交点的横坐标为4,则另一个交点的坐标为 ;
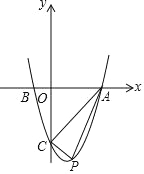
(4) 如图,二次函数 y=mx2﹣2mx+n 的图象经过点 A(3,0),连接 AC,点 P 是抛物线位于线段 AC 下方图象上的任意一点,求△PAC 面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 是⊙
是⊙![]() 上一点,
上一点, ![]() 与过点
与过点![]() 的切线垂直,垂足为点
的切线垂直,垂足为点![]() ,直线
,直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,弦
,弦![]() 平分∠
平分∠![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
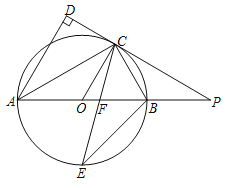
(1)求证: ![]() 平分∠
平分∠![]() ;
;
(2)求证:PC=PF;
(3)若![]() ,AB=14,求线段
,AB=14,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,按要求完成下面的问题:
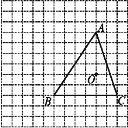
(1)以图中的O为位似中心,将△ABC作位似变换且缩小到原来的一半,得到△A'B'C',再把△A'B'C'绕点B'逆时针旋转90°得到△A″B'C″;
(2)求点A→A'→A″所经过的路线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+b与反比例函数y=![]() 的图形交于A(a,4)和B(4,1)两点.
的图形交于A(a,4)和B(4,1)两点.
(1)求b,k的值;
(2)在第一象限内,当一次函数y=﹣x+b的值大于反比例函数y=![]() 的值时,直接写出自变量x的取值范围;
的值时,直接写出自变量x的取值范围;
(3)将直线y=﹣x+b向下平移m个单位,当直线与双曲线只有一个交点时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在矩形ABCD中,对角线AC与BD相交于点O,过点C作BD的平行线,过点D作AC的平行线,两线交于点P.
①求证:四边形CODP是菱形.
②若AD=6,AC=10,求四边形CODP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
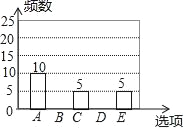
【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.
选项 | 频数 | 频率 |
A | 10 | m |
B | n | 0.2 |
C | 5 | 0.1 |
D | p | 0.4 |
E | 5 | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com