
【题目】已知二次函数 y=mx2﹣2mx+n 的图象经过(0,﹣3).
(1)n= _____________;
(2) 若二次函数 y=mx2﹣2mx+n 的图象与 x 轴有且只有一个交点,求 m 值;
(3) 若二次函数 y=mx2﹣2mx+n 的图象与平行于 x 轴的直线 y=5 的一个交点的横坐标为4,则另一个交点的坐标为 ;
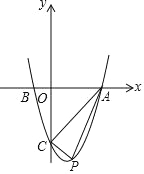
(4) 如图,二次函数 y=mx2﹣2mx+n 的图象经过点 A(3,0),连接 AC,点 P 是抛物线位于线段 AC 下方图象上的任意一点,求△PAC 面积的最大值.
【答案】(1)-3;(2)m=﹣3;(3)(﹣2,5);(4)当a=![]() 时,△PAC的面积取最大值,最大值为
时,△PAC的面积取最大值,最大值为![]()
【解析】
(1)将(0,-3)代入二次函数解析式中即可求出n值;
(2)由二次函数图象与x轴只有一个交点,利用根的判别式△=0,即可得出关于m的一元二次方程,解之取其非零值即可得出结论;
(3)根据二次函数的解析式利用二次函数的性质可找出二次函数图象的对称轴,利用二次函数图象的对称性即可找出另一个交点的坐标;
(4)将点A的坐标代入二次函数解析式中可求出m值,由此可得出二次函数解析式,由点A、C的坐标,利用待定系数法可求出直线AC的解析式,过点P作PD⊥x轴于点D,交AC于点Q,设点P的坐标为(a,a2-2a-3),则点Q的坐标为(a,a-3),点D的坐标为(a,0),根据三角形的面积公式可找出S△ACP关于a的函数关系式,配方后即可得出△PAC面积的最大值.
解:(1)∵二次函数y=mx2﹣2mx+n的图象经过(0,﹣3),
∴n=﹣3.
故答案为:﹣3.
(2)∵二次函数y=mx2﹣2mx﹣3的图象与x轴有且只有一个交点,
∴△=(﹣2m)2﹣4×(﹣3)m=4m2+12m=0,
解得:m1=0,m2=﹣3.
∵m≠0,
∴m=﹣3.
(3)∵二次函数解析式为y=mx2﹣2mx﹣3,
∴二次函数图象的对称轴为直线x=﹣![]() =1.
=1.
∵该二次函数图象与平行于x轴的直线y=5的一个交点的横坐标为4,
∴另一交点的横坐标为1×2﹣4=﹣2,
∴另一个交点的坐标为(﹣2,5).
故答案为:(﹣2,5).
(4)∵二次函数y=mx2﹣2mx﹣3的图象经过点A(3,0),
∴0=9m﹣6m﹣3,
∴m=1,
∴二次函数解析式为y=x2﹣2x﹣3.
设直线AC的解析式为y=kx+b(k≠0),
将A(3,0)、C(0,﹣3)代入y=kx+b,得:
![]() ,解得:
,解得:![]() ,
,
∴直线AC的解析式为y=x﹣3.
过点P作PD⊥x轴于点D,交AC于点Q,如图所示.
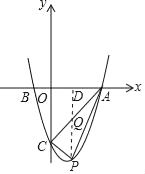
设点P的坐标为(a,a2﹣2a﹣3),则点Q的坐标为(a,a﹣3),点D的坐标为(a,0),
∴PQ=a﹣3﹣(a2﹣2a﹣3)=3a﹣a2,
∴S△ACP=S△APQ+S△CPQ=![]() PQOD+
PQOD+![]() PQAD=﹣
PQAD=﹣![]() a2+
a2+![]() a=﹣
a=﹣![]() (a﹣
(a﹣![]() )2+
)2+![]() ,
,
∴当a=![]() 时,△PAC的面积取最大值,最大值为
时,△PAC的面积取最大值,最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)求购买一个足球、一个篮球各需多少元?
(2)根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列四个关于是否成反比例的命题,判断它们的真假.
(1)面积一定的等腰三角形的底边长和底边上的高成反比例;
(2)面积一定的菱形的两条对角线长成反比例;
(3)面积一定的矩形的两条对角线长成反比例;
(4)面积一定的直角三角形的两直角边长成比例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了![]() ,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
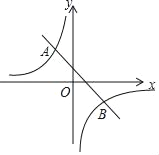
【题目】如图,已知A(m,2),B(2,n)是一次函数y=﹣x+1的图象与反比例函数y=![]() (k≠0)图象的两个交点.
(k≠0)图象的两个交点.
(1)求反比例函数的解析式;
(2)根据图象,请直接写出关于x的不等式﹣x+1<![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣![]() x>
x>![]() 的解集;
的解集;
(3)将直线l1:y=- ![]() x沿y向上平移后的直线l2与反比例函数y=
x沿y向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
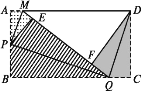
【题目】如图,矩形纸片ABCD,P是AB的中点,Q是BC上一动点,△BPQ沿PQ折叠,点B落在点E处,延长QE交AD于M点,连接PM.
(1)求证:△PAM≌△PEM;
(2)当DQ⊥PQ时,将△CQD沿DQ折叠,点C落在线段EQ上点F处.
①求证:△PAM∽△DCQ;
②如果AM=1,sin∠DMF=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点I为△ABC的内心,连AI交△ABC的外接圆于点D,若AI=2CD,点E为弦AC的中点,连接EI,IC,若IC=6,ID=5,则IE的长为_____.
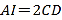
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com