
【题目】等边三角形的内切圆半径、外接圆半径和高的比为( )
A. 3:2:1 B. 1:2:3 C. 2:3:1 D. 3:1:2
【答案】B
【解析】
如图,⊙O 为△ABC 的内切圆,设⊙O 的半径为 r,作 AH⊥BC 于 H,利用等边三角形的性质得 AH 平分∠BAC,则可判断点 O 在 AH 上,所以 OH=r,连接 OB,再证明
OA=OB=2r,则 AH=3r,所以 OH:OA:AH=1:2:3.
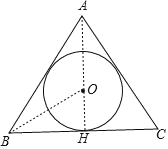
解: 如图,⊙O 为△ABC 的内切圆,设⊙O 的半径为 r,作 AH⊥BC 于 H,
∵△ABC 为等边三角形,
∴AH 平分∠BAC,即∠BAH=30°,
∴点 O 在 AH 上,
∴OH=r, 连接 OB,
∵⊙O 为△ABC 的内切圆,
∴∠ABO=∠CBO=30°,
∴OA=OB,
在 Rt△OBH 中,OB=2OH=2r,
∴AH=2r+r=3r,
∴OH:OA:AH=1:2:3,
即等边三角形的内切圆半径、外接圆半径和高的比为 1:2:3.
故选:B.


科目:初中数学 来源: 题型:
【题目】如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
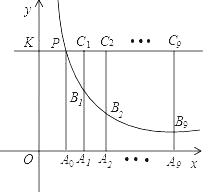
【题目】如图,直线y=k和双曲线y=![]() 相交于点P,过P点作PA0垂直x轴,垂足为A0,x轴上的点A0、A1、A2、…A9的横坐标是连续的整数,过点A1、A2、…A9分别作x轴的垂线,与双曲线y=
相交于点P,过P点作PA0垂直x轴,垂足为A0,x轴上的点A0、A1、A2、…A9的横坐标是连续的整数,过点A1、A2、…A9分别作x轴的垂线,与双曲线y=![]() (x>0)及直线y=k分别交于点B1、B2、…B9,C1、C2、…C9,则
(x>0)及直线y=k分别交于点B1、B2、…B9,C1、C2、…C9,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学三次到某超市购买A、B两种商品,其中仅有一次是有折扣的,购买数量及消费金额如下表:
类别 次数 | 购买A商品数量(件) | 购买B商品数量(件) | 消费金额(元) |
第一次 | 4 | 5 | 320 |
第二次 | 2 | 6 | 300 |
第三次 | 5 | 7 | 258 |
解答下列问题:
(1)第 次购买有折扣;
(2)求A、B两种商品的原价;
(3)若购买A、B两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买A、B两种商品共10件,在(3)中折扣数的前提下,消费金额不超过200元,求至少购买A商品多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=mx2﹣2mx+n 的图象经过(0,﹣3).
(1)n= _____________;
(2) 若二次函数 y=mx2﹣2mx+n 的图象与 x 轴有且只有一个交点,求 m 值;
(3) 若二次函数 y=mx2﹣2mx+n 的图象与平行于 x 轴的直线 y=5 的一个交点的横坐标为4,则另一个交点的坐标为 ;
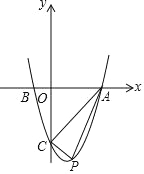
(4) 如图,二次函数 y=mx2﹣2mx+n 的图象经过点 A(3,0),连接 AC,点 P 是抛物线位于线段 AC 下方图象上的任意一点,求△PAC 面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
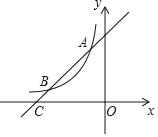
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求a,k的值及点B的坐标;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,直接写出点P的坐标.
S△BOC,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,按要求完成下面的问题:
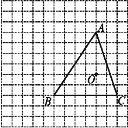
(1)以图中的O为位似中心,将△ABC作位似变换且缩小到原来的一半,得到△A'B'C',再把△A'B'C'绕点B'逆时针旋转90°得到△A″B'C″;
(2)求点A→A'→A″所经过的路线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
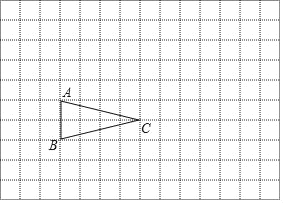
【题目】如图,方格纸中每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)请在方格纸上建立平面直角坐标系,使点A、C的坐标分别为(2,3)、(6,2),并写出点B的坐标;
(2)以原点O为位似中心,在第一象限内将△ABC放大,相似比为2,画出放大后的△A'B'C';
(3)直接写出B′C′与AC的交点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com