
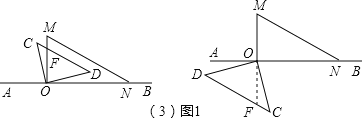
【题目】如图,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)将图①中的三角板OMN沿BA方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图③,MN与CD相交于点E,求∠CEN的度数;
(3)将图①中的三角尺COD绕点O按每秒15°的速度沿顺时针防线旋转一周,在旋转过程中,在第几秒时,MN恰好与CD平行;第几秒时,MN恰好与直线CD垂直.

【答案】(1) 105°;(2) 135°; (3)5或17;11或23
【解析】
(1)根据三角形的内角和定理列式计算即可得解;
(2)根据内错角相等,两直线平行判断出MN∥BC,再根据两直线平行,同旁内角互补解答;
(3)作出图形,然后分两种情况求出旋转角,再根据时间=旋转角÷速度计算即可得解.
解:(1)在△CEN中,
∠CEN=180°-∠DCN-∠MNO=180°-45°-30°=105°
(2)∵∠BON=∠N=30°,
∴MN∥CB,
∴∠CEN=180°-∠DCO=180°-45°=135°
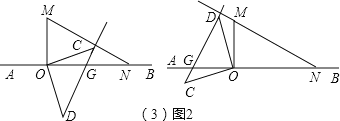
(3)如图1,CD在AB上方时,设OM与CD相交于F,
∵CD∥MN,
∴∠OFD=∠M=60°,
在△ODF中,∠MOD=180°-∠D-∠OFD,
=180°-45°-60°,
=75°,
∴旋转角为75°,
t=75°÷15°=5秒;
CD在AB的下方时,设直线OM与CD相交于F,
∵CD∥MN,
∴∠DFO=∠M=60°,
在△DOF中,∠DOF=180°-∠D-∠DFO=180°-45°-60°=75°,
∴旋转角为75°+180°=255°,
t=255°÷15°=17秒;
综上所述,第5或17秒时,边CD恰好与边MN平行;
如图2,CD在OM的右边时,设CD与AB相交于G,
∵CD⊥MN,
∴∠NGC=90°-∠MNO=90°-30°=60°,
∴∠CON=∠NGC-∠OCD=60°-45°=15°,
∴旋转角为180°-∠CON=180°-15°=165°,
t=165°÷15°=11秒,
CD在OM的左边时,设CD与AB相交于G,
∵CD⊥MN,
∴∠NGD=90°-∠MNO=90°-30°=60°,
∴∠AOC=∠NGD-∠C=60°-45°=15°,
∴旋转角为360°-∠AOC=360°-15°=345°,
t=345°÷15°=23秒,
综上所述,第11或23秒时,直线CD恰好与直线MN垂直.


科目:初中数学 来源: 题型:
【题目】你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答会告诉你方法.
(1)阅读下列材料:
问题:利用一元一次方程将![]() 化成分数.
化成分数.
解:设![]() .
.
方程两边都乘以10,可得![]() .
.
由![]() 和
和![]() ,可得
,可得![]() 即
即![]() .(请你体会将方程两边都乘以10起到的作用)
.(请你体会将方程两边都乘以10起到的作用)
解得![]() ,即
,即![]() .
.
填空:将0.![]() 写成分数形式为 .
写成分数形式为 .
(2)请你仿照上述方法把小数1.![]() 化成分数,要求写出利用一元一次方程进行解答的过程.
化成分数,要求写出利用一元一次方程进行解答的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,点E,F分别是线段BC,DC上的动点.当△AEF的周长最小时,则∠EAF的度数为( )
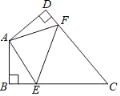
A. 90°B. 80°C. 70°D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC和△A1B1C1关于x轴成轴对称,画出△A1B1C1
(2)点C1的坐标为_________,△ABC的面积为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).
(1)写出点A的坐标.
(2)画出△OAB绕点O顺时针旋转90°后的△OA1B1;
(3)求点A旋转到点A1所经过的路线长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知长方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,由
上,由![]() 往
往![]() 运动,速度为
运动,速度为![]() ,运动时间为
,运动时间为![]() 秒,将
秒,将![]() 沿着
沿着![]() 翻折至
翻折至![]() ,点
,点![]() 对应点为
对应点为![]() ,
,![]() 所在直线与边
所在直线与边![]() 交与点
交与点![]() ,
,
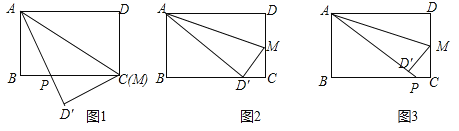
(1)如图![]() ,当
,当![]() 时,求证:
时,求证:![]() ;
;
(2)如图![]() ,当
,当![]() 为何值时,点
为何值时,点![]() 恰好落在边
恰好落在边![]() 上;
上;
(3)如图![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市道路美化工程招标,经测算:甲队 12 天完成的工程量是乙队 9 天完成的工程量的2 倍,甲队干 20 天比乙队干 15 天多完成的工程量占总工程量的![]() .
.
(1)求甲、乙两队一天各完成此项工程的量?
(2)甲队施工一天需付工程款 1.5 万元,乙队施工一天需付工程款 0.8 万元,若要求完成此项工程的工程款不超过 81 万元,则乙队最少施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF.
(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B是数轴上的两个点,它们分别表示的数是![]() 和1. 点A与点B之间的距离表示为AB.
和1. 点A与点B之间的距离表示为AB.
(1)AB= .
(2)点P是数轴上A点右侧的一个动点,它表示的数是![]() ,满足
,满足![]() ,求
,求![]() 的值.
的值.
(3)点C为6. 若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.请问:![]() 的值是否随着运动时间t(秒)的变化而改变? 若变化,请说明理由;若不变,请求其值.
的值是否随着运动时间t(秒)的变化而改变? 若变化,请说明理由;若不变,请求其值.
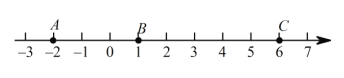
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com