
【题目】(发现与思考)如图①∠ACB=∠ADB=90°那么点D在经过A,B,C三点的圆上,如图②,如果∠ACB=∠ADB=α(α≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上?
(应用)若四边形ABCD中,AD∥BC,∠CAD=90°,点E在边AB上,CE⊥DE.
(1)作∠ADF=∠AED,交CA的延长线于点F(如图④),求证:DF为Rt△ACD的外接圆的切线;
(2)如图⑤,点G在BC的延长线上,∠BGE=∠BAC,已知sin∠AED=![]() ,AD=1,求DG的长.
,AD=1,求DG的长.
【答案】发现与思考:点D即不在⊙O内,也不在⊙O外,点D在⊙O上;应用:(1)见解析;(2)DG=2![]() .
.
【解析】
发现与思考:假设点D在⊙O内,利用圆周角定理及三角形外角的性质,可证得与条件相矛盾的结论,从而可得点D在⊙O上;
应用:(1)作出Rt△ACD的外接圆,由发现与思考可得点E在⊙O上,则可证得∠ACD=∠FDA,又因为∠ACD+∠ADC=90°,于是有∠FDA+∠ADC=90°,即可证得DF为Rt△ACD的外接圆的切线;
(2)根据发现与思考可得点G在过C、A、E三点的圆上,即⊙O,进而易证四边形ACGD是矩形,根据已知条件解直角三角形ACD可得AC的长,即DG的长.
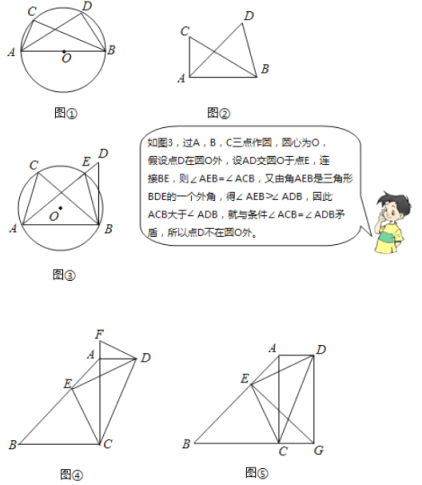
解:发现与思考:如图1,假设点D在⊙O内,延长AD交⊙O于点E,连接BE,则∠AEB=∠ACB,
∵∠ADB是△BDE的外角,
∴∠ADB>∠AEB,
∴∠ADB>∠ACB,
因此,∠ADB>∠ACB与条件∠ACB=∠ADB矛盾,
所以点D也不在⊙O内,
因为点D即不在⊙O内,也不在⊙O外,
所以点D在⊙O上;
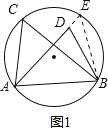
应用:(1)如图2,取CD的中点O,则点O是Rt△ACD的外心,
∵∠CAD=∠DEC=90°,
∴点E在⊙O上,
∴∠ACD=∠AED,
∵∠FDA=∠AED,
∴∠ACD=∠FDA,
∵∠DAC=90°,
∴∠ACD+∠ADC=90°,
∴∠FDA+∠ADC=90°,
∴OD⊥DF,
∴DF为Rt△ACD的外接圆的切线;
(2)∵∠BGE=∠BAC,
∴点G在过C、A、E三点的圆上,如图3,
又∵过C、A、E三点的圆是Rt△ACD的外接圆,即⊙O,
∴点G在⊙O上,
∵CD是直径,
∴∠DGC=90°,
∵AD∥BC,
∴∠ADG=90°
∵∠DAC=90°
∴四边形ACGD是矩形,
∴DG=AC,
∵sin∠AED=![]() ,∠ACD=∠AED,
,∠ACD=∠AED,
∴sin∠ACD=![]() ,
,
在Rt△ACD中,AD=1,
∴CD=3,
∴AC=![]() ,
,
∴DG=AC=![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (x>0)和一次函数y=mx+n的图象过格点(网格线的交点)B、P.
(x>0)和一次函数y=mx+n的图象过格点(网格线的交点)B、P.
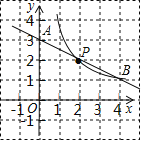
(1)求反比例函数和一次函数的解析式;
(2)观察图象,直接写出一次函数值大于反比例函数值时x的取值范围是: .
(3)在图中用直尺和2B铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:
①四个顶点均在格点上,且其中两个顶点分别是点O,点P;
②矩形的面积等于k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
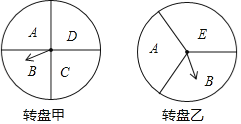
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受9折优惠的概率为多少;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
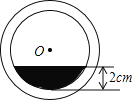
【题目】将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
A.(![]() π﹣4
π﹣4![]() )cm2B.(
)cm2B.(![]() π﹣8
π﹣8![]() )cm2
)cm2
C.(![]() π﹣4
π﹣4![]() )cm2D.(
)cm2D.(![]() π﹣2
π﹣2![]() )cm2
)cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
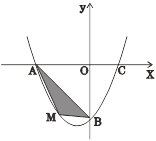
【题目】在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为![]() ,△AMB的面积为S.求S关于
,△AMB的面积为S.求S关于![]() 的函数关系式,并求出S的最大值.
的函数关系式,并求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点分别为A(﹣2,1),B(﹣1,3),C(﹣2,4).
(1)画出△ABC关于原点O对称的△A1B1C1,并写出点B1的坐标;
(2)画出△ABC绕原点O顺时针方向旋转90°得到的△A2B2C2,并写出点A2的坐标.
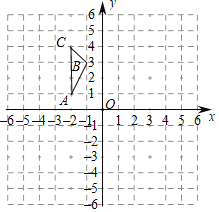
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣
x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣![]() +bx+c经过A,B两点.
+bx+c经过A,B两点.
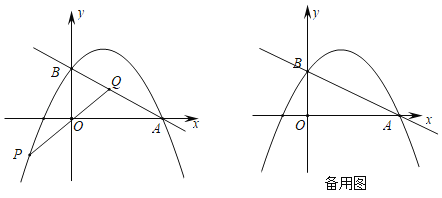
(1)求抛物线的解析式;
(2)点P在抛物线上,点Q在直线AB上,当P,Q关于原点O成中心对称时,求点Q的坐标;
(3)点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
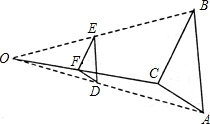
【题目】按如下方法,将△ABC的三边缩小的原来的![]() ,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是( )
,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是( )
①△ABC与△DEF是位似图形②△ABC与△DEF是相似图形
③△ABC与△DEF的周长比为1:2④△ABC与△DEF的面积比为4:1.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
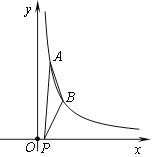
【题目】如图,双曲线![]() (x>0)经过点A(1,6)、点B(2,n),点P的坐标为(t,0),且-1≤t<3,则△PAB的最大面积为_______________.
(x>0)经过点A(1,6)、点B(2,n),点P的坐标为(t,0),且-1≤t<3,则△PAB的最大面积为_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com