
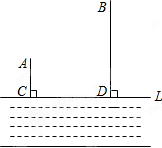
 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,已知AC=200米,BD=600米,且CD=600米.
如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,已知AC=200米,BD=600米,且CD=600米.分析 (1)要求牧童行驶距离最短的饮水点P,除非AP、BP的和为两定点之间的距离,也即是P在两定点F、B的连线上.
(2)作BE⊥BD交CA的延长线于点E,求得AE=BD+AC=600+200=800m,BE=CD=600m,然后根据勾股定理求出FB的长.
解答 解:(1)作点A关于L的对称点F,连接BF交CD于点P,则点P为所求,此时PA+PB=BF,BF就是最短路程.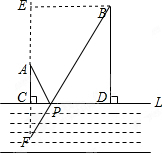
(2)作BE⊥BD交CA的延长线于点E,如图所示,
由题意得AE=BD+AC=600+200=800m,BE=CD=600m
由勾股定理得:BF=$\sqrt{E{F}^{2}+B{E}^{2}}$=1000m
所以最短路程为1000米.
点评 本题考查了最短路径的数学问题.这类问题的解答依据是“两点之间,线段最短”,可以利用对称的性质,通过等线段代换,将所求路线长转化为两定点之间的距离.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
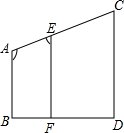 填写完整过程:
填写完整过程:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
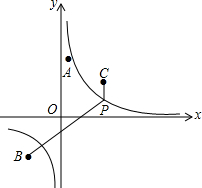 如图,点A,B,C的坐标分别为(1,5),(-4,-4),(4,4),点P为双曲线y=$\frac{8}{x}$(x>0)上一个动点.
如图,点A,B,C的坐标分别为(1,5),(-4,-4),(4,4),点P为双曲线y=$\frac{8}{x}$(x>0)上一个动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com