
 填写完整过程:
填写完整过程:分析 由垂直可证明AB∥CD,再条件可证明AB∥EF,利用平行的传递性可证明CD∥EF,据此填空即可.
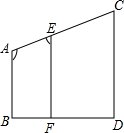
解答 证明:∵AB⊥BD,CD⊥BD( 已知),
∴AB∥CD( 垂直于同一直线的两条直线互相平行),
∵∠1+∠2=180°( 已知),
∴AB∥EF( 同旁内角互补,两直线平行),
∴CD∥EF( 平行于同一条直线的两条直线互相平行).
故答案为:已知;垂直于同一直线的两条直线互相平行;已知;AB;EF;同旁内角互补,两直线平行;平行于同一条直线的两直线互相平行.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.


科目:初中数学 来源: 题型:解答题
 列方程解应用题:如图,在长为32m,宽为20m的矩形地面上,修筑同样宽的两条平行且与另一条相互垂直的道路,余下的六个空白的部分作为耕地,要使得耕地的面积为504m2,道路的宽应为多少?
列方程解应用题:如图,在长为32m,宽为20m的矩形地面上,修筑同样宽的两条平行且与另一条相互垂直的道路,余下的六个空白的部分作为耕地,要使得耕地的面积为504m2,道路的宽应为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
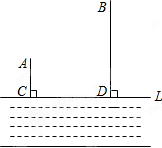 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,已知AC=200米,BD=600米,且CD=600米.
如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,已知AC=200米,BD=600米,且CD=600米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
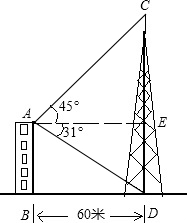 如图,佛山电视塔离小明家60米,小明从自家的阳台眺望电视塔,并测得塔尖C的仰角是45°,而塔底部D的俯角是31°,求佛山电视塔CD的高度.(tan31°=0.600,结果精确到1米)
如图,佛山电视塔离小明家60米,小明从自家的阳台眺望电视塔,并测得塔尖C的仰角是45°,而塔底部D的俯角是31°,求佛山电视塔CD的高度.(tan31°=0.600,结果精确到1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com