
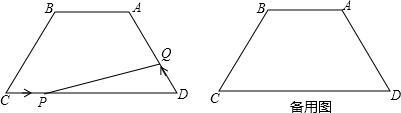
分析 (1)过点B作BM⊥CD于点M,利用等腰梯形ABCD中,AB=4,CD=9,∠C=60°,即可得出CM的长,进而得出BC=AD的长;
(2)当PQ⊥AD时,得出∠QPD=30°,DQ=$\frac{1}{2}$PD,即可得出答案;
(3)可通过求△PDQ的面积与x的函数关系式来得出△PDQ的最大值.由于P、Q速度相同,因此CP=QD=x,那么可用x表示出PD,而△PQD中,PD边上的高=QD•sin60°,由此可根据三角形的面积公式求出S△PQD与x之间的函数关系式,可根据函数的性质求出S的最大值以及对应的x的值.
(4)假设存在这样的M点,那么DM就是PQ的垂直平分线,可得出QD=PD、PM=AM,然后证PM=PD即可.根据(2)中得出PD、DQ的表达式,可求出x=$\frac{9}{2}$,即P是CD的中点,不难得出△QPD为等边三角形,因此∠QPD=∠C=60°,因此PQ∥CM,即∠DMC=90°,在直角三角形DMC中,P为斜边CD的中点,因此PM=PD,即可得出四边形PDQM是菱形.那么此时根据BM=BC-CM可求出BM的长.
解答 解:(1)如图1,过点B作BM⊥CD于点M,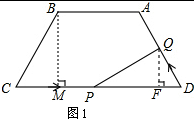
∵等腰梯形ABCD中,AB=4,CD=9,∠C=60°,
∴CM=$\frac{1}{2}$×(9-4)=$\frac{5}{2}$,∠CBM=30°,
∴BC=AD=2CM=5;
(2)当PQ⊥AD时,
∵BC=AD,∠C=60°
∴∠D=60°,
∴∠QPD=30°,
∴DQ=$\frac{1}{2}$PD,
$\frac{1}{2}$(9-x)=x,
解得:x=3,
∴当x为3时,PQ⊥AD;
(3)如图2,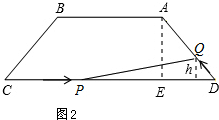
∵CP=x,h为PD边上的高,依题意,
△PDQ的面积S可表示为:
S=$\frac{1}{2}PD•h=\frac{1}{2}(9-x)•x•sin6{0}^{°}$=$\frac{\sqrt{3}}{4}(9x-{x}^{2})=-\frac{\sqrt{3}}{4}(x-\frac{9}{2})^{2}+\frac{81\sqrt{3}}{16}$,(0<x≤5),
由题意知0<x≤5,
当x=$\frac{9}{2}$时(满足0<x≤5),${S}_{最大值}=\frac{81\sqrt{3}}{16}$.
(4)如图3,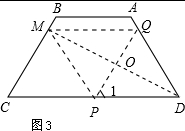
存在满足条件的点M,则PD必须等于DQ.
于是9-x=x,x=$\frac{9}{2}$.
此时,点P、Q的位置如图4所示,△PDQ恰为等边三角形.
过点D作DO⊥PQ于点O,延长DO交BC于点M,连接PM、QM,则DM垂直平分PQ,
∴MP=MQ.
易知∠1=∠C.
∴PQ∥BC.
又∵DO⊥PQ,
∴MC⊥MD
∴MP=$\frac{1}{2}$CD=PD
即MP=PD=DQ=QM
∴四边形PDQM是菱形
所以存在满足条件的点M,且BM=BC-MC=5-$\frac{9}{2}$=$\frac{1}{2}$.
点评 本题是一道压轴题,也是一道开放探索题,第(3)问是条件开放,第(4)问是结论开放.本题既考查了学生的分析作图能力,又考查学生综合运用平行线、等腰梯形、等边三角形、菱形、二次函数等知识.这里设计了一个开放的、动态的数学情境,为学生灵活运用基础知识、分析问题、解决问题留下了广阔的探索、创新的思维空间.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
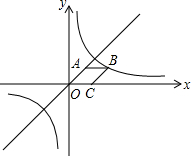 如图,点C在x轴的正半轴上,菱形OCBA的面积为$\sqrt{2}$,点B在双曲线y=$\frac{k}{x}$上,点A在直线y=x上,则k的值为( )
如图,点C在x轴的正半轴上,菱形OCBA的面积为$\sqrt{2}$,点B在双曲线y=$\frac{k}{x}$上,点A在直线y=x上,则k的值为( )| A. | 1+$\frac{{\sqrt{2}}}{2}$ | B. | 1+$\sqrt{2}$ | C. | $\sqrt{2}$+2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
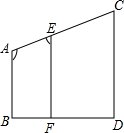 填写完整过程:
填写完整过程:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com