
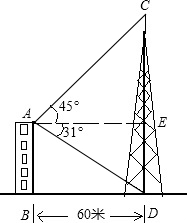
 如图,佛山电视塔离小明家60米,小明从自家的阳台眺望电视塔,并测得塔尖C的仰角是45°,而塔底部D的俯角是31°,求佛山电视塔CD的高度.(tan31°=0.600,结果精确到1米)
如图,佛山电视塔离小明家60米,小明从自家的阳台眺望电视塔,并测得塔尖C的仰角是45°,而塔底部D的俯角是31°,求佛山电视塔CD的高度.(tan31°=0.600,结果精确到1米) 分析 先根据题意得出四边形ABDE是矩形,从而得出AE=BD=CE=60米,在Rt△AED中,再根据tan31°=$\frac{ED}{AE}$,求出DE的值,最后根据CD=CE+DE,即可求出佛山电视塔CD的高度.
解答 解:根据题意可得:四边形ABDE是矩形,
则AE=BD=CE=60米,
在Rt△AED中,
∵tan31°=$\frac{ED}{AE}$,
∴DE=AE•tan31°=60×0.600=36.0,
∴CD=CE+DE=60+36.0=96(米).
答:佛山电视塔的高度CD约为96米.
点评 此题主要考查解直角三角形的应用.要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.


科目:初中数学 来源: 题型:解答题
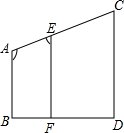 填写完整过程:
填写完整过程:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
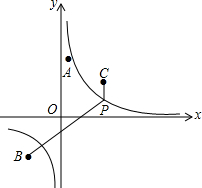 如图,点A,B,C的坐标分别为(1,5),(-4,-4),(4,4),点P为双曲线y=$\frac{8}{x}$(x>0)上一个动点.
如图,点A,B,C的坐标分别为(1,5),(-4,-4),(4,4),点P为双曲线y=$\frac{8}{x}$(x>0)上一个动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
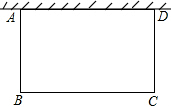 小明和小强利用假期去农场参加社会实践,正遇到农场拟建一个养鸡场,养鸡场的一面靠墙(墙足够长),计划中的建筑材料可建围墙的总长为100m.小明将鸡场设计成矩形,并算出鸡场的面积为1200m2,请你求出此时鸡场的长和宽分别是多少米?
小明和小强利用假期去农场参加社会实践,正遇到农场拟建一个养鸡场,养鸡场的一面靠墙(墙足够长),计划中的建筑材料可建围墙的总长为100m.小明将鸡场设计成矩形,并算出鸡场的面积为1200m2,请你求出此时鸡场的长和宽分别是多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com