
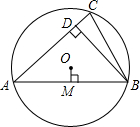
 如图,点C是⊙O优弧AB上的一动点(异于A、B两点),OM⊥AB于点M.连接AC、BC,作BD⊥AC于点D.点C运动到某一位置时OM=CD,此时∠CAB的度数为30°.
如图,点C是⊙O优弧AB上的一动点(异于A、B两点),OM⊥AB于点M.连接AC、BC,作BD⊥AC于点D.点C运动到某一位置时OM=CD,此时∠CAB的度数为30°. 分析 连结OA、OB.根据等腰三角形的性质得出∠BOM=$\frac{1}{2}$∠AOB,AM=BM=$\frac{1}{2}$AB,由圆周角定理得出∠C=$\frac{1}{2}$∠AOB,那么∠C=∠BOM.再利用ASA证明△BCD≌△BOM,根据全等三角形对应边相等得出BD=BM,则BD=$\frac{1}{2}$AB,由sin∠CAB=$\frac{BD}{AB}$=$\frac{1}{2}$,求出∠CAB=30°.
解答 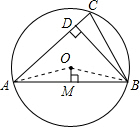 解:连结OA、OB.
解:连结OA、OB.
∵OA=OB,OM⊥AB于点M,
∴∠BOM=$\frac{1}{2}$∠AOB,AM=BM=$\frac{1}{2}$AB,
∵∠C=$\frac{1}{2}$∠AOB,
∴∠C=∠BOM.
在△BCD与△BOM中,
$\left\{\begin{array}{l}{∠C=∠BOM}\\{CD=OM}\\{∠BDC=∠BMO=90°}\end{array}\right.$,
∴△BCD≌△BOM(ASA),
∴BD=BM,
∴BD=$\frac{1}{2}$AB,
∴sin∠CAB=$\frac{BD}{AB}$=$\frac{1}{2}$,
∴∠CAB=30°.
故答案为30°.
点评 本题考查了全等三角形的判定与性质,圆周角定理,等腰三角形的性质,锐角三角函数定义及特殊角的三角函数值,准确作出辅助线构造全等三角形得出BD=BM是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 太阳光强弱 | B. | 水的温度 | C. | 所晒时间 | D. | 热水器 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线a,b被直线c所截,则下列说法中错误的是( )
如图,直线a,b被直线c所截,则下列说法中错误的是( )| A. | ∠1与∠3是对顶角 | B. | ∠2与∠3是邻补角 | C. | ∠2与∠4是同位角 | D. | ∠1与∠4是内错角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-4)2=6 | B. | (x-2)2=4 | C. | (x-2)2=0 | D. | (x-2)2=10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
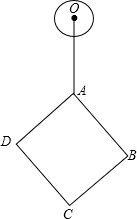 如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,在旋转过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )
如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,在旋转过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )| A. | 3次 | B. | 4次 | C. | 5次 | D. | 6次 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
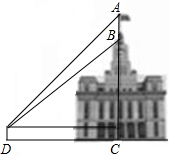 如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度约为7.2m.(结果精确到0.1m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度约为7.2m.(结果精确到0.1m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com