
【题目】如图,△ABC是边长为4个等边三角形,D为AB边的中点,以CD为直径画圆,则图中阴影部分的面积为(结果保留π). 
【答案】2.5 ![]() ﹣π
﹣π
【解析】解:过点O作OE⊥AC于点E,连接FO,MO, ∵△ABC是边长为4的等边三角形,D为AB边的中点,以CD为直径画圆,
∴CD⊥AB,∠ACD=∠BCD=30°,AC=BC=AB=4,
∴∠FOD=∠DOM=60°,AD=BD=2,
∴CD=2 ![]() ,则CO=DO=
,则CO=DO= ![]() ,
,
∴EO= ![]() ,EC=EF=
,EC=EF= ![]() ,则FC=3,
,则FC=3,
∴S△COF=S△COM= ![]() ×
× ![]() ×3=
×3= ![]() ,
,
S扇形OFM= ![]() =π,
=π,
S△ABC= ![]() ×CD×4=4
×CD×4=4 ![]() ,
,
∴图中影阴部分的面积为:4 ![]() ﹣2×
﹣2× ![]() ﹣π=2.5
﹣π=2.5 ![]() ﹣π.
﹣π.
故答案为:2.5 ![]() ﹣π.
﹣π.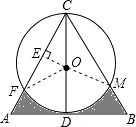
根据等边三角形的性质以及勾股定理得出△COF,△COM,△ABC以及扇形FOM的面积,进而得出答案.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时点P的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y= ![]() 的图像上,OA=1,OC=6,试求出正方形ADEF的边长.
的图像上,OA=1,OC=6,试求出正方形ADEF的边长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在北海市创建全国文明城活动中,需要20名志愿者担任“讲文明树新风”公益广告宣传工作,其中男生8人,女生12人.
(1)若从这20人中随机选取一人作为“展板挂图”讲解员,求选到女生的概率;
(2)若“广告策划”只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲担任,否则乙担任.试问这个游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在左边托盘A(固定)中放置一个重物,在右边托盘B(可左右移动)中放置一定质量的砝码,可使得仪器左右平衡,改变托盘B与支撑点M的距离,记录相应的托盘B中的砝码质量,得到下表: 
托盘B与点O的距离x(cm) | 10 | 15 | 20 | 25 | 30 |
托盘B中的砝码质量y(g) | 30 | 20 | 15 | 12 | 10 |
(1)把上表中(x,y)的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出其余的点,并用一条光滑曲线连接起来;观察所画的图像,猜测y与x之间的函数关系,求出该函数解析式;
(2)当托盘B向左移动(不超过点M)时,应往托盘B中添加砝码还是减少砝码?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=5,CD=2.以A为圆心,AD为半径的圆与BC边相切于点M,与AB交于点E,将扇形A﹣DME剪下围成一个圆锥,则圆锥的高为( ) 
A.1
B.4
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】罗平、昆明两地相距240千米,甲车从罗平出发匀速开往昆明,乙车同时从昆明出发匀速开往罗平,两车相遇时距罗平90千米,已知乙车每小时比甲车多行驶30千米,求甲、乙两车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=x﹣2与反比例函数y= ![]() 的图象交于A、B两点.
的图象交于A、B两点. 
(1)求A、B两点的坐标;
(2)观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;
(3)坐标原点为O,求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com