
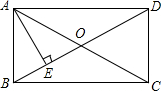
 如图,在矩形ABCD中,AE⊥BD于E,AC与BD相交于O点,DE=3BE.
如图,在矩形ABCD中,AE⊥BD于E,AC与BD相交于O点,DE=3BE.分析 (1)由矩形的性质得出OB=OD=$\frac{1}{2}$BD,OA=OC=$\frac{1}{2}$AC,AC=BD,证出OA=OB,易证得△OAB是等边三角形,继而求得∠1的度数;
(2)由△OAB是等边三角形,易求得∠ADE=30°,又由AD=12cm,由含30°角的直角三角形的性质求得AE的长,由三角函数求出AB的长即可.
解答 解:(1)∵四边形ABCD是矩形,
∴OB=OD=$\frac{1}{2}$BD,OA=OC=$\frac{1}{2}$AC,AC=BD,
∴OA=OB,
∵DE=3BE,
∴BE=OE,
∵AE⊥BD,
∴AB=OA,
∴OA=AB=OB,
即△OAB是等边三角形,
∴∠BAO=60°,
∴∠1=$\frac{1}{2}$∠BAO=30°;
(2)∵△OAB是等边三角形,
∴∠ABD=60°,
∴∠ADE=90°-∠ABD=30°,
∵AE⊥BD,AD=12cm,
∴AE=$\frac{1}{2}$AD=6cm,AB=AD•tan30°=12×$\frac{\sqrt{3}}{3}$=4$\sqrt{3}$(cm).
点评 此题考查了矩形的性质、等边三角形的判定与性质、含30°角的直角三角形的性质、三角函数.此题难度不大,证明△AOB是等边三角形是解决问题的关键.


 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:选择题
 抛物线y=-x2+bx+c的部分图象如图所示,对称轴是直线x=-1,与x轴交于点(1,0),若y<0,则x的取值范围是( )
抛物线y=-x2+bx+c的部分图象如图所示,对称轴是直线x=-1,与x轴交于点(1,0),若y<0,则x的取值范围是( )| A. | x>0 | B. | x>1 | C. | x<-3或x>1 | D. | D-3<x<1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D.
如图,在ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com