
【题目】如图1,已知在矩形ABCD中,AD=10,E是CD上一点,且DE=5,点P是BC上一点,PA=10,∠PAD=2∠DAE.
(1)求证:∠APE=90°;
(2)求AB的长;
(3)如图2,点F在BC边上且CF=4,点Q是边BC上的一动点,且从点C向点B方向运动.连接DQ,M是DQ的中点,将点M绕点Q逆时针旋转90°,点M的对应点是M′,在点Q的运动过程中,①判断∠M′FB是否为定值?若是说明理由.②求AM′的最小值.

【答案】(1)见解析;(2)AB=8;(3)①∠M′FB为定值,理由见解析;②当AM'⊥FM'时,AM'的值最小,AM'=2![]() .
.
【解析】
(1)由SAS证明△APE≌△ADE得出∠APE=∠D=90°即可;
(2)由全等三角形的性质得出PE=DE=5,设BP=x,则PC=10﹣x,证明△ABP∽△PCE,得出![]() ,得出AB=20﹣2x,CE=
,得出AB=20﹣2x,CE=![]() x,由AB=CD得出方程,解方程即可得出结果;
x,由AB=CD得出方程,解方程即可得出结果;
(3)①作MG⊥B于G,M'H⊥BC于H,证明△HQM'≌△GMQ得出HM'=GQ,QH=MG=4,设HM'=x,则CG=GQ=x,FG=4﹣x,求出QF=GQ﹣FG=2x﹣4,得出FH=QH+QF=2x,由三角函数得出tan∠∠M′FB=![]() ,即可得出结论;②当AM'⊥FM'时,AM'的值最小,延长HM'交DA延长线于N,则NH=AB=8,NM'=8﹣x,AN=BH=HQ﹣BQ=2x﹣6,同①得:△ANM'∽△M'HF,得出
,即可得出结论;②当AM'⊥FM'时,AM'的值最小,延长HM'交DA延长线于N,则NH=AB=8,NM'=8﹣x,AN=BH=HQ﹣BQ=2x﹣6,同①得:△ANM'∽△M'HF,得出![]() ,解得:x=4,得出AN=2,NM'=4,在Rt△ANM'中,由勾股定理即可得出结果.
,解得:x=4,得出AN=2,NM'=4,在Rt△ANM'中,由勾股定理即可得出结果.
(1)证明:∵四边形ABCD是矩形,
∴BC=AD=10,AB=CD,∠B=∠C=∠D=90°,
∵AD=10,PA=10,∠PAD=2∠DAE,
∴AP=AD,∠PAE=∠DAE,
在△APE和△ADE中,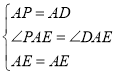 ,
,
∴△APE≌△ADE(SAS),
∴∠APE=∠D=90°;
(2)由(1)得:△APE≌△ADE,
∴PE=DE=5,
设BP=x,则PC=10﹣x,
∵∠B=90°,∠APE=90°,
∴∠BAP+∠APB=90°,∠APB+∠CPE=90°,
∴∠BAP=∠CPE,
∴△ABP∽△PCE,
∴![]() ,即
,即![]() =2,
=2,
∴AB=20﹣2x,CE=![]() x,
x,
∵AB=CD,
∴20﹣2x=5+![]() x,
x,
解得:x=6,
∴AB=20﹣2x=8;
(3)①∠M′FB为定值,理由如下:
作MG⊥B于G,M'H⊥BC于H,如图2所示:
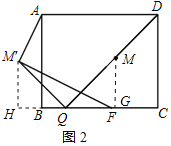
则MG∥CD,∠H=∠MGQ=90°,
∴∠QMG+∠MQG=90°,
∵M是DQ的中点,
∴QG=CG,
∴MG是△CDQ的中位线,
∴MG=![]() CD=
CD=![]() AB=4,
AB=4,
由旋转的性质,QM'=QM,∠M'QM=90°,
∴∠HQM'+∠MQG=90°,
∴∠HQM'=∠QMG,
在△HQM'和△GMQ中,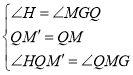 ,
,
∴△HQM'≌△GMQ(ASA),
∴HM'=GQ,QH=MG=4,
设HM'=x,则CG=GQ=x,
∴FG=4﹣x,
∴QF=GQ﹣FG=2x﹣(4﹣x)=2x﹣4,
∴FH=QH+QF=2x,
∴tan∠M′FB=![]() =
=![]() ,
,
∴∠M′FB为定值;
②当AM'⊥FM'时,AM'的值最小,延长HM'交DA延长线于N,如图3所示:
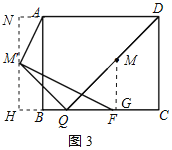
则NH=AB=8,NM'=8﹣x,AN=BH=HQ﹣BQ=4﹣(10﹣2x)=2x﹣6,
同①得:△ANM'∽△M'HF,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:x=4,
∴AN=2,NM'=4,
在Rt△ANM'中,由勾股定理得:AM'=![]() .
.


科目:初中数学 来源: 题型:
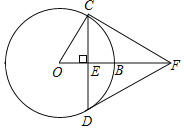
【题目】如图,点B是⊙O上一点,弦CD⊥OB于点E,过点C的切线交OB的延长线于点F,连接DF,
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为2,∠CFD=60°,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
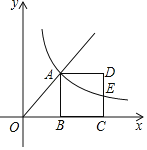
【题目】如图,点A是射线y═![]() (x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=
(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=![]() 交CD边于点E,则
交CD边于点E,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解全校学生上学的交通方式,该校九年级![]() 班的4名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查
班的4名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查![]() 按
按![]() 骑自行车
骑自行车![]() 、
、![]() 乘公交车
乘公交车![]() 、
、![]() 步行
步行![]() 、
、![]() 乘私家车
乘私家车![]() 、
、![]() 其他方式
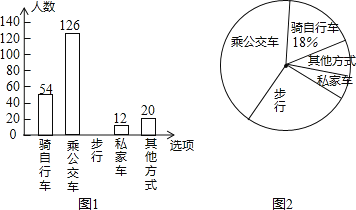
其他方式![]() 设置选项,要求被调查同学从中单选,并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
设置选项,要求被调查同学从中单选,并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
![]() 本次接受调查的总人数是______人,并把条形统计图补充完整;
本次接受调查的总人数是______人,并把条形统计图补充完整;
![]() 在扇形统计图中,“乘私家车的人数所占的百分比是______,“其他方式”所在扇形的圆心角度数是______度;
在扇形统计图中,“乘私家车的人数所占的百分比是______,“其他方式”所在扇形的圆心角度数是______度;
![]() 已知这4名同学中有2名女同学,要从中选两名同学汇报调查结果,请你用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.
已知这4名同学中有2名女同学,要从中选两名同学汇报调查结果,请你用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
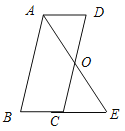
【题目】已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD ≌ △EOC;
(2)连接AC,DE,当∠B![]() ∠AEB
∠AEB![]() _______ °时,四边形ACED是正方形?请说明理由.
_______ °时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
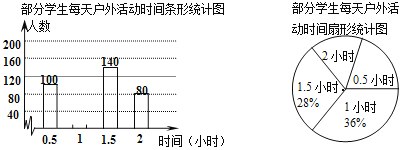
【题目】为了解学生参加户外活动的情况,某市教育行政部门对部分学生参加户外活动的时间进行了抽样调查,并将调查结果绘制成下列两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)这次抽样共调查了 名学生,并补全条形统计图;
(2)计算扇形统计图中表示户外活动时间0.5小时的扇形圆心角度数;
(3)求出本次调查学生参加户外活动的平均时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育老师统计了七年级甲、乙两个班女生的身高,并绘制了以下不完整的统计图.

请根据图中信息,解决下列问题:
(1)两个班共有女生多少人?
(2)将频数分布直方图补充完整;
(3)求扇形统计图中![]() 部分所对应的扇形圆心角度数;
部分所对应的扇形圆心角度数;
(4)身高在![]() 的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
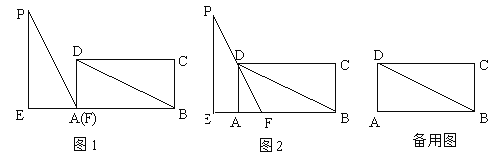
【题目】如图1,在矩形ABCD中,DB=6,AD=3,在Rt△PEF中,∠PEF=90°,EF=3,PF=6,△PEF(点F和点A重合)的边EF和矩形的边AB在同一直线上.现将Rt△PEF从A以每秒1个单位的速度向射线AB方向匀速平移,当点F与点B重合时停止运动,设运动时间为t秒,
解答下列问题:
(1)如图1,连接PD,填空:∠PFD= ,四边形PEAD的面积是 ;
(2)如图2,当PF经过点D时,求 △PEF运动时间t的值;
(3)在运动的过程中,设△PEF与△ABD重叠部分面积为S,请求出S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,以O为圆心,OA为半径的圆与BC相切与点B,与OC相交于点D.
中,以O为圆心,OA为半径的圆与BC相切与点B,与OC相交于点D.

(1)求![]() 的度数.
的度数.
(2)如图,点E在⊙O上,连接CE与⊙O交于点F,若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com