
 如图是2009年7月的台历,用“
如图是2009年7月的台历,用“ ”形框数,每次框出5个数.
”形框数,每次框出5个数.分析 (1)如果框出的数最大是24,那么这5个数是10、16、17、18、24,求这5个数的平均数即可;
(2)根据要求可知一行、第二行与第三行可以框住3个不同的和,第二行、第三行与第四行可以框住5个不同的和,第三行、第四行与第五行可以框住5个不同的和,由此可得出一共可以框出多少个不同的和;
(3)要使框出的5个数中,必须有1个数在周五,那么第一行、第二行与第三行有2种框法,第二行、第三行与第四行有2种框法;第三行、第四行与第五行有2种框法,由此可得出一共有多少种不同的框法.
解答 解:(1)(10+16+17+18+24)÷5
=85÷5
=17;
(2)因为第一行、第二行与第三行可以框住3个不同的和,
第二行、第三行与第四行可以框住5个不同的和,
第三行、第四行与第五行可以框住5个不同的和,
所以一共可以框住不同数的和的个数是:3+5+5=13;
(3)要使框出的5个数中,必须有1个数在周五,那么第一行、第二行与第三行有2种框法,
第二行、第三行与第四行有2种框法;
第三行、第四行与第五行有2种框法,
由此得出一共有2+2+2=6种不同的框法.
答:(1)如果框出的数最大是24,那么框住的5个数的平均数是17.
(2)一共可以框住13个不同数的和.
(3)框出的5个数中,必须有1个数在周五,那么有6种不同的框法.
点评 本题考查了探索规律问题,根据台历表的特点和要求探索出规律是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某小区内有一块长、宽比为2:1的矩形空地,计划在该空地上修筑两条宽为2m的互相垂直的小路,余下的四块小矩形空地铺成草坪,如果四块草坪的面积之和为312m2,请求出原来大矩形空地的长和宽.
如图,某小区内有一块长、宽比为2:1的矩形空地,计划在该空地上修筑两条宽为2m的互相垂直的小路,余下的四块小矩形空地铺成草坪,如果四块草坪的面积之和为312m2,请求出原来大矩形空地的长和宽.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
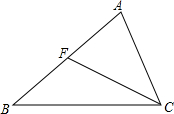 如图,F是△ABC的AB边上一点,下列结论正确的个数是( )
如图,F是△ABC的AB边上一点,下列结论正确的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
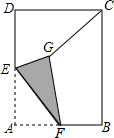 如图,在矩形ABCD中,AD=6,CD=4,AD的中点为E,点F是AB边上一点(不与A、B重合),连接EF,把∠A沿EF折叠,使点A落在点G处,连接CG.则线段CG的取值范围是$\frac{2}{5}$$\sqrt{37}$<CG<2$\sqrt{13}$.
如图,在矩形ABCD中,AD=6,CD=4,AD的中点为E,点F是AB边上一点(不与A、B重合),连接EF,把∠A沿EF折叠,使点A落在点G处,连接CG.则线段CG的取值范围是$\frac{2}{5}$$\sqrt{37}$<CG<2$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | mn或-mn | B. | -mn | C. | mn | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com