
| A. | mn或-mn | B. | -mn | C. | mn | D. | 2 |
分析 因为mn<0,分两种情况探讨:m>0,n<0;m<0,n>0;化简探讨得出答案即可.
解答 解:∵mn<0,$\frac{1}{m^2}+\frac{1}{n^2}$=1,
∴m>0,n<0或m<0,n>0,$\frac{1}{{m}^{2}}$=1-$\frac{1}{{n}^{2}}$或$\frac{1}{{n}^{2}}$=1-$\frac{1}{{m}^{2}}$或m2+n2=m2n2,
∴当m>0,n<0时,
m$\sqrt{1-\frac{1}{m^2}}-n\sqrt{1-\frac{1}{n^2}}$
=-$\frac{m}{n}$-$\frac{n}{m}$
=-$\frac{{m}^{2}+{n}^{2}}{mn}$
=-mn;
当m<0,n>0,
m$\sqrt{1-\frac{1}{m^2}}-n\sqrt{1-\frac{1}{n^2}}$
=$\frac{m}{n}$+$\frac{n}{m}$
=$\frac{{m}^{2}+{n}^{2}}{mn}$
=mn.
故选:A.
点评 此题考查二次根式的化简求值,分两种情况探讨,把式子灵活变形是解决问题的关键.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
 如图是2009年7月的台历,用“
如图是2009年7月的台历,用“ ”形框数,每次框出5个数.
”形框数,每次框出5个数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
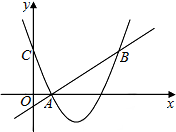 如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B
如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B查看答案和解析>>
科目:初中数学 来源: 题型:选择题
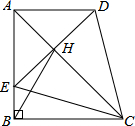 在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论正确的个数是( )
在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
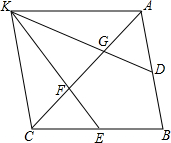 已知△ABC,D,E分别为AB,BC上的中点,F,G为AC的三等分点.连接EF,DG交于K.连接AK,CK,求证:四边形ABCK为平行四边形.
已知△ABC,D,E分别为AB,BC上的中点,F,G为AC的三等分点.连接EF,DG交于K.连接AK,CK,求证:四边形ABCK为平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com