
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
 如图,某小区内有一块长、宽比为2:1的矩形空地,计划在该空地上修筑两条宽为2m的互相垂直的小路,余下的四块小矩形空地铺成草坪,如果四块草坪的面积之和为312m2,请求出原来大矩形空地的长和宽.
如图,某小区内有一块长、宽比为2:1的矩形空地,计划在该空地上修筑两条宽为2m的互相垂直的小路,余下的四块小矩形空地铺成草坪,如果四块草坪的面积之和为312m2,请求出原来大矩形空地的长和宽.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
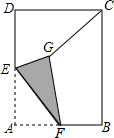 如图,在矩形ABCD中,AD=6,CD=4,AD的中点为E,点F是AB边上一点(不与A、B重合),连接EF,把∠A沿EF折叠,使点A落在点G处,连接CG.则线段CG的取值范围是$\frac{2}{5}$$\sqrt{37}$<CG<2$\sqrt{13}$.
如图,在矩形ABCD中,AD=6,CD=4,AD的中点为E,点F是AB边上一点(不与A、B重合),连接EF,把∠A沿EF折叠,使点A落在点G处,连接CG.则线段CG的取值范围是$\frac{2}{5}$$\sqrt{37}$<CG<2$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | mn或-mn | B. | -mn | C. | mn | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com