
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上的高,过点
边上的高,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() .
.
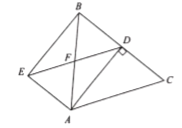
(1)求证:四边形![]() 是矩形;
是矩形;
(2)求四边形![]() 的周长.
的周长.
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数![]() 的大致图象;
的大致图象;
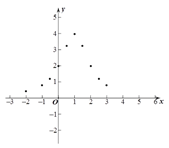
(4)结合函数图象,请写出函数![]() 的一条性质:______________________.
的一条性质:______________________.
(5)解决问题:如果函数![]() 与直线y=a的交点有2个,那么a的取值范围是______________ .
与直线y=a的交点有2个,那么a的取值范围是______________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
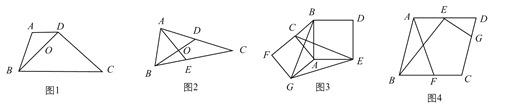
【题目】如图1,我们把对角线互相垂直的四边形叫做对垂四边形.
观察发现:如图1,对垂四边形ABCD四边存在数量为: AD2+BC2=AB2+CD2.
应用发现:如图2,若AE,BD是△ABC的中线,AE⊥BD,垂足为O,AC=4,BC=6,求AB=
应用知识:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=![]() ,AB=
,AB=![]() 求GE长.
求GE长.
拓展应用:如图4,在平行四边形ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=4,AB=3,求AF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象交
的图象交![]() 轴和
轴和![]() 轴于点
轴于点![]() 和
和![]() ;另一个一次函数
;另一个一次函数![]() 的图象交
的图象交![]() 轴和
轴和![]() 轴于点
轴于点![]() 和
和![]() ,且两个函数的图象交于点
,且两个函数的图象交于点![]()
(1)当![]() ,
,![]() 为何值时,
为何值时,![]() 和
和![]() 的图象重合;
的图象重合;
(2)当![]() 的面积为
的面积为![]() 时,求线段
时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
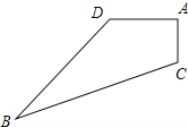
【题目】已知某实验中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草坪,经测量∠A=90°,AC=3m,BD=12m,CB=13m,DA=4m,若每平方米草坪需要300元,间学校需要投入多少资金买草坪?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD//BC,∠A=∠C,CD=2AD,BE⊥AD于点E,F为CD的中点,连接EF、BF.
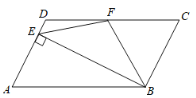
(1)求证:四边形ABCD是平行四边形;
(2)求证:BF平分∠ABC;
(3)请判断△BEF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 3 | 6 | 10 | … |
日销售量(m件) | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格-每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“七·一”党的生日,某校准备组织师生共310人参加一次大型公益活动,租用4辆大客车和6辆小客车恰好全部坐满,已知每辆大客车的座位数比小客车多15个.
(1)求每辆大客车和小客车的座位数;
(2)经学校统计,实际参加活动人数增加了40人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为使所有参加活动的师生均有座位,最多租用小客车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求解一元一次方程,需要根据等式的基本性质,把方程转化为x=a的形式;求解二元一次方程组,需要通过消元把它转化为一元一次方程来解;求解三元一次方程组,需要把它转化为二元一次方程组来解;求解一元二次方程,需要把它转化为两个一元一次方程来解;求解分式方程,需要通过去分母把它转化为整式方程来解,各类方程的解法不尽相同,但是它们都用到一种共同的基本数学思想﹣转化,即把未知转化为已知来求解.
用“转化“的数学思想,我们还可以解一些新的方程.
例如,解一元三次方程x3+x2﹣2x=0,通过因式分解把它转化为x(x2+x﹣2)=0,通过解方程x=0和x2+x﹣2=0,可得原方程x3+x2﹣2x=0的解.
再例如,解根号下含有来知数的方程:![]() =x,通过两边同时平方把它转化为2x+3=x2,解得:x1=3,x2=﹣1.因为2x+3≥0,且x≥0,所以x=﹣1不是原方程的根,x=3是原方程的解.
=x,通过两边同时平方把它转化为2x+3=x2,解得:x1=3,x2=﹣1.因为2x+3≥0,且x≥0,所以x=﹣1不是原方程的根,x=3是原方程的解.
(1)问题:方程x3+x2﹣2x=0的解是x1=0,x2= ,x3= .
(2)拓展:求方程![]() =x﹣1的解;
=x﹣1的解;
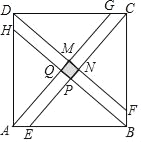
(3)应用:在一个边长为1的正方形中构造一个如图所示的正方形;在正方形ABCD边上依次截取AE=BF=CG=DH=![]() ,连接AG,BH,CE,DF,得到正方形MNPQ,若小正方形MNPQ(图中阴影部分)的边长为
,连接AG,BH,CE,DF,得到正方形MNPQ,若小正方形MNPQ(图中阴影部分)的边长为![]() ,求n的值.
,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com