【题目】为迎接“七·一”党的生日，某校准备组织师生共310人参加一次大型公益活动，租用4辆大客车和6辆小客车恰好全部坐满，已知每辆大客车的座位数比小客车多15个.
（1）求每辆大客车和小客车的座位数；
（2）经学校统计，实际参加活动人数增加了40人，学校决定调整租车方案，在保持租用车辆总数不变的情况下，为使所有参加活动的师生均有座位，最多租用小客车多少辆？
金博士一点全通系列答案科目：初中数学 来源： 题型：
【题目】如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动（与A、C不重合），Q是CB延长线上一点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．
（1）当∠BQD=30°时，求AP的长；
（2）当运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，点D在AB上，在下列四个条件中：①∠ACD=∠B；②∠ADC=∠ACB；③AC2=ADAB；④ABCD=ADCB，能满足△ADC与△ACB相似的条件是（ ）
A．①、②、③ B．①、③、④ C．②、③、④ D．①、②、④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB=90°，过B,C两点的⊙O交AC于点D，交AB于点E，连接EO并延长交⊙O于点F.连接BF,CF.若∠EDC=135°,CF=
,则AE2+BE2的值为 （ ）
A. 8 B. 12 C. 16 D. 20
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了解同学们每月零花钱数额，校园小记者随机调查了本校部分学生，并根据调查结果绘制出如下不完整的统计图表.
请根据以上图表，解答下列问题：
（1）这次被调查的人数共有 人，a= ;
（2）计算并补全频数分布直方图；
（3）请估计该校1500名学生中每月零花钱数额低于90元的人数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠AOB＝20°，点M、N分别是边OA、OB上的定点，点P，Q分别是边OB、OA上的动点，记∠MPQ＝α，∠PQN＝β，当MP＋PQ＋QN最小时，则β－α的值为（ ）
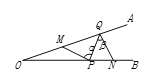
A.19°B.40°C.9°D.29
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点A（0，b）、点B（a，0）、点D（d，0）且a、b、c满足
．DE⊥x轴且∠BED=∠ABD，BE交y轴于点C，AE交x轴于点F．
（1）求点A、B、D的坐标；
（2）求点C、E、F的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
（1）直接写出点A，B，C关于x轴对称的点A1，B1，C1的坐标；.
（2）在图中作出△ABC关于y轴对称图形△A2B2C2．
（3）计算△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如果三角形有一边上的中线长恰好等于这边的长，那么这个三角形叫“恰等三角形”，这条中线叫“恰等中线”．
（直角三角形中的“恰等中线”）
（1）如图1，在△ABC中，∠C＝90°，AC＝
，BC＝2，AM为△ABC的中线．求证：AM是“恰等中线”．
（等腰三角形中的“恰等中线”）
（2）已知，等腰△ABC是“恰等三角形”，AB＝AC＝20，求底边BC的平方．
（一般三角形中的“恰等中线”）
（3）如图2，若AM是△ABC的“恰等中线”，则BC2，AB2，AC2之间的数量关系为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
