
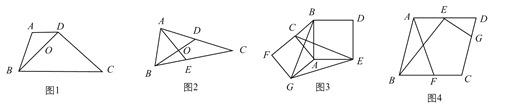
【题目】如图1,我们把对角线互相垂直的四边形叫做对垂四边形.
观察发现:如图1,对垂四边形ABCD四边存在数量为: AD2+BC2=AB2+CD2.
应用发现:如图2,若AE,BD是△ABC的中线,AE⊥BD,垂足为O,AC=4,BC=6,求AB=
应用知识:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=![]() ,AB=
,AB=![]() 求GE长.
求GE长.
拓展应用:如图4,在平行四边形ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=4,AB=3,求AF的长
【答案】应用发现:![]() ;应用知识:3;拓展应用:
;应用知识:3;拓展应用:![]()
【解析】
应用发现:连接DE,构成对垂四边形,再根据对垂四边形ABCD四边存在数量关系进行计算即可;
应用知识:先证明CE⊥BG得到四边形CGEB是对垂四边形,再根据结论进行计算即可;
拓展应用:连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,连接PH,先证明四边形APHE是对垂四边形和EP、AH是△AFE的中线,再根据对垂四边形的性质求得AP的长度,从而求得AF的长度.
应用发现:
连接DE,如图所示:
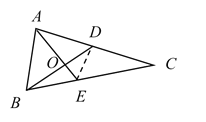
∵AE,BD是△ABC的中线,AC=4,BC=6,
∴AD=2,BE=3,DE=![]() ,
,
∵AE⊥BD,垂足为O,
∴四边形ABED是对垂四边形,
∴AB2+DE2=AD2+BE2,
∴AB2+![]() =22+32,
=22+32,
∴AB=![]() ;
;
应用知识:
连接CG、BE,如图所示:
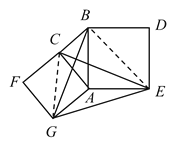
∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△GAB和△CAE中,
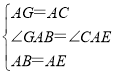 ,
,
∴△GAB≌△CAE,
∴∠ABG=∠AEC,又∠AEC+∠AME=90°,
∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是对垂四边形,
∴CG2+BE2=CB2+GE2,
∵AC=![]() ,AB=
,AB=![]() ,
,
∴BC=1,CG=![]() ,BE=
,BE=![]() ,
,
∴22+![]() =12+GE2,
=12+GE2,
∴GE=3;
拓展应用:
(3)如图,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,连接PH,

∵点E、G分别是AD,CD的中点,
∴EG∥AC,
∵BE⊥EG,
∴BE⊥AC,
∴四边形APHE是对垂四边形,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=4,
∴∠EAH=∠FCH,
∵E,F分别是AD,BC的中点,
∴AE=![]() AD,BF=
AD,BF=![]() BC,
BC,
∴AE=BF![]() AD=2,
AD=2,
又∵AE∥BF,
∴四边形ABFE是平行四边形,
∴EF=AB=3,AP=PF,
∴EP分别是△AFE的中线,
在△AEH和△CFH中,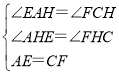 ,
,
∴△AEH≌△CFH(AAS),
∴EH=FH,
∴AH分别是△AFE的中线,
∴PH=![]() ,EH=
,EH=![]() ,
,
∵四边形APHE是对垂四边形,
∴PH2+AE2=EH2+AP2,
∴12+22=![]() +AP2,
+AP2,
∴AP=![]() ,
,
又∵EP分别是△AFE的中线,
∴AF=2AP=![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】下列说法中不正确的是( )
A.抛掷一枚硬币,硬币落地时正面朝上是随机事件
B.把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件
C.一个盒子中有白球![]() 个,红球6个,黑球
个,红球6个,黑球![]() 个(每个球除了颜色外都相同).如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么
个(每个球除了颜色外都相同).如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么![]() 与
与![]() 的和是6
的和是6
D.任意打开七年级下册数学教科书,正好是100页是确定事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与应用:在学习几何时,我们可以通过分离和构造基本图形,将几何“模块”化.例如在相似三角形中,![]() 字形是非常重要的基本图形,可以建立如下的“模块”(如图①):
字形是非常重要的基本图形,可以建立如下的“模块”(如图①):


![]() .
.
(1)请就图①证明上述“模块”的合理性;
(2)请直接利用上述“模块”的结论解决下面两个问题:
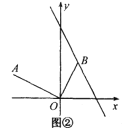
①如图②,已知点![]() ,点
,点![]() 在直线
在直线![]() 上运动,若
上运动,若![]() ,求此时点
,求此时点![]() 的坐标;
的坐标;
②如图③,过点![]() 作
作![]() 轴与
轴与![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,求点
,求点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们规定:当x取任意一个值时,x对应的函数值分别为y1和y2,若y1≠y2,取y1和y2中较小值为M;若y1=y2,记M=y1=y2.①当x>2时,M=y2;②当x<0时,M随x的增大而增大;③使得M大于4的x的值不存在;④若M=2,则x=1.上述结论正确的是_____(填写所有正确结论的序号).
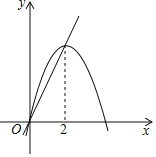
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
①试说明BE·AD=CD·AE;
②根据图形特点,猜想![]() 可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com