
【题目】如图,点E是正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.

【答案】(1)证明见解析(2)△CEF是直角三角形
【解析】
(1)由正方形的性质、等腰三角形的性质可得AB=CB,BE=BF,再通过等量相减,即可得出∠ABF=∠CBE,由SAS即可证出△ABF≌△CBE;
(2)求∠CEF=90°,即可证出△CEF是直角三角形.
证明:(1)∵四边形ABCD是正方形,
∴AB=CB,∠ABC=90°,
∵△EBF是等腰直角三角形,其中∠EBF=90°,
∴BE=BF,
∴∠ABC﹣∠CBF=∠EBF﹣∠CBF,
∴∠ABF=∠CBE.
在△ABF和△CBE中,有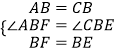 ,
,
∴△ABF≌△CBE(SAS).
(2)△CEF是直角三角形.理由如下:
∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°,
∴∠AFB=180°﹣∠BFE=135°,
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°,
∴∠CEF=∠CEB﹣∠FEB=135°﹣45°=90°,
∴△CEF是直角三角形.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,网格中有格点△ABC与△DEF.
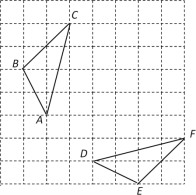
(1)△ABC与△DEF是否全等?(不说理由.)
(2)△ABC与△DEF是否成轴对称?(不说理由.)
(3)若△ABC与△DEF成轴对称,请画出它的对称轴l.并在直线l上画出点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC,BD相交于点O,动点E以每秒1个单位长度的速度从点A出发沿AC方向运动,点F同时以每秒1个单位长度的速度从点C出发沿CA方向运动,若AC=12,BD=8,则经过________秒后,四边形BEDF是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
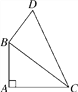
【题目】如图所示,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.
(1)连接BC,求BC的长;
(2)求四边形ABDC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形OABC的边OA在x轴上,点B的坐标为(8,4),P是对角线OB上的一个动点,点D(0,1)在y轴上,当PC+PD最短时,点P的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).

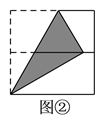


A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:-1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AC是一根垂直于地面的木杆,B是木杆上的一点,且AB=2米,D是地面上一点,AD=3米.在B处有甲、乙两只猴子,D处有一堆食物.甲猴由B往下爬到A处再从地面直奔D处,乙猴则向上爬到木杆顶C处腾空直扑到D处,如果两猴所经过的距离相等,则木杆的长为( )
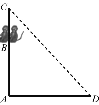
A. ![]() m B. 2
m B. 2![]() m C. 3
m C. 3![]() m D. 5 m
m D. 5 m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com