
【题目】如图,在四边形ABCD中,AD//BC,∠A=∠C,CD=2AD,BE⊥AD于点E,F为CD的中点,连接EF、BF.
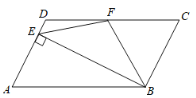
(1)求证:四边形ABCD是平行四边形;
(2)求证:BF平分∠ABC;
(3)请判断△BEF的形状,并证明你的结论.
【答案】(1)见解析;(2)见解析;(3)ΔBEF为等腰三角形,见解析.
【解析】
(1)由平行线的性质得出∠A+∠ABC=180°,由已知得出∠C+∠ABC=180°,证出AB//BC,即可得出四边形ABCD是平行四边形;
(2)由平行四边形的性质得出BC=AD,AB//CD,得出∠CFB=∠ABF,由已知得出CF=BC,得出∠CFB=∠CBF,证出∠ABF=∠CBF即可;
(3)作FG⊥BE于G,证出FG/AD//BC,得出EG=BG,由线段垂直平分线的性质得出EF=BF即可.
解:(1)证明:∵AD∥BC,
∴∠A+∠ABC=180°:
∵∠A=∠C
∴∠C+∠ABC=180°
∴AB∥CD
∴四边形ABCD是平行四边形
(2)证明:
∵F点为CD中点
∴CD=2CF
∴CD=2AD
∴CF=AD=BC
∴∠CFB=∠CBF
∴CD∥AB
∴∠CFB=∠FBA
∴∠FBA=∠CBF
∴BF平分∠ABC
(3)ΔBEF为等腰三角形
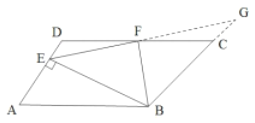
理由:如图,延长EF交B延长线于点G
∴DA∥BG
∴∠G=∠DEF
∵F为DC中点
∴DF=CF
又∵∠DFE=∠CFG
∴ΔDFE≌ΔCFG(AAS)
∴FE=FG
∵AD∥BC,BE⊥AD
∴BE⊥CD
∴∠EBG=90°
在RtΔEBG中,F为BG中点
∴BF=![]() EG=EF
EG=EF
∴ΔBEF为等腰三角形。


科目:初中数学 来源: 题型:
【题目】如图,已知DE是直角梯形ABCD的高,将△ADE沿DE翻折,腰AD恰好经过腰BC的中点,则AE:BE等于( )
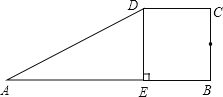
A.2:1 B.1:2 C.3:2 D.2:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1所示,在Rt△ABC中,∠ACB=90°,AC=BC,点D在斜边AB上,点E在直角边BC上,若∠CDE=45°,求证:△ACD∽△BDE.
(2)如图2所示,在矩形ABCD中,AB=4cm,BC=10cm,点E在BC上,连接AE,过点E作EF⊥AE交CD(或CD的延长线)于点F.
①若BE:EC=1:9,求CF的长;
②若点F恰好与点D重合,请在备用图上画出图形,并求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的内接四边形ABCD中,AC,BD是它的对角线,AC的中点I是△ABD的内心.求证:
(1)OI是△IBD的外接圆的切线;
(2)AB+AD=2BD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①有一个角是![]() 的等腰三角形是等边三角形;②如果三角形的一个外角平分线平行三角形的一边,那么这个三角形是等腰三角形;③三角形三边的垂直平分线的交点与三角形三个顶点的距离相等;④有两个角相等的等腰三角形是等边三角形.其中正确的个数有( )
的等腰三角形是等边三角形;②如果三角形的一个外角平分线平行三角形的一边,那么这个三角形是等腰三角形;③三角形三边的垂直平分线的交点与三角形三个顶点的距离相等;④有两个角相等的等腰三角形是等边三角形.其中正确的个数有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( )
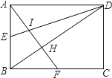
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果经销商上月份销售一种新上市的水果,平均售价为10元/千克,月销售量为1000千克.经市场调查,若将该种水果价格调低至x元/千克,则本月份销售量y(千克)与x(元/千克)之间符合一次函数关系,并且得到了表中的数据:
价格x(元/千克) | 7 | 5 |
价格y(千克) | 2000 | 4000 |
(1)求y与x之间的函数解析式;
(2)已知该种水果上月份的成本价为5元/千克,本月份的成本价为4元/千克,要使本月份销售该种水果所获利润比上月份增加20%,同时又要让顾客得到实惠,那么该种水果价格每千克应调低至多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com