
����Ŀ����1����ͼ1��ʾ����Rt��ABC�У���ACB��90�㣬AC��BC����D��б��AB�ϣ���E��ֱ�DZ�BC�ϣ�����CDE��45������֤����ACD�ס�BDE��
��2����ͼ2��ʾ���ھ���ABCD�У�AB��4cm��BC��10cm����E��BC�ϣ�����AE������E��EF��AE��CD����CD���ӳ��ߣ��ڵ�F��
����BE��EC��1��9����CF�ij���
������Fǡ�����D�غϣ����ڱ���ͼ�ϻ���ͼ�Σ�����BE�ij���

���𰸡���1������������2����CF��![]() ����BE�ij�Ϊ2cm��8cm
����BE�ij�Ϊ2cm��8cm
��������
��1���ɵ���ֱ������������֪��A=��B=45�㡢��ACD+��ADC=135����������CDE=45��֪��ADC+��BDE=135�����ݴ˵ó���BDE=��ACD���Ӷ���֤��
��2�����ɾ��ε����ʼ�EF��AE֪��BAE+��AEB=90�㡢��CEF+��BEA=90�����ó���BAE=��CEF������֤��BAE�ס�CEF��![]() =
=![]() ���ݴ˼���ɵã�
���ݴ˼���ɵã�
����BE=xcm����������BAE�ס�CEF���ݴ�֪![]() =
=![]() ����
����![]() =
=![]() ����֮����.
����֮����.
�⣺��1������Rt��ABC�У���ACB=90�㣬AC=BC��
���A=��B=45�㣬
���ACD+��ADC=135�㣬
�ߡ�CDE=45�㣬
���ADC+��BDE=135�㣬
���BDE=��ACD��
���ACD�ס�BDE��
��2���١��ı���ABCD�Ǿ��Σ�
���B=��C=90�㣬
���BAE+��AEB=90�㣬
�ߡ�AEF=90�㣬
���CEF+��BEA=90�㣬
���BAE=��CEF��
���BAE�ס�CEF��
��![]() =
=![]() ��
��
��BE��EC=1��9��
��BE=![]() BC=1cm��CE=9cm��
BC=1cm��CE=9cm��
��![]() =
=![]() ��CF=
��CF=![]() ��
��
����ͼ��ʾ����BE=xcm��
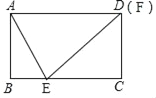
�ɢٵ���BAE�ס�CEF��
��![]() =
=![]() ����
����![]() =
=![]() ��
��
�������ã�x2��10x+16=0��
��ã�x1=2��x2=8��
����BE�ij�Ϊ2cm��8cm��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һԪ���η���ax2+bx+c=0��a��0������˵����ȷ���ǣ�������
����a��c��ţ���ax2+bx+c=0��a��0��һ����ʵ������
����b2��4ac��0����ax2+bx+c=0��a��0��һ�������������ʵ������
����b=a+c����ax2+bx+c=0��a��0������������ȵ�ʵ������
��������ax2+bx+c=0��a��0��������������ͬ����ô����cx2+bx+a=0��c��0������������Ҳ��ͬ��
A. ֻ���٢� B. ֻ���٢ڢ� C. ֻ���٢� D. ֻ���ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ����
����![]() Ϊ
Ϊ![]() ����ƽ����һ�㣬����
����ƽ����һ�㣬����![]() �ֱ���
�ֱ���![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() .
.

����![]() ��
��![]() �ϣ���ͼ�٣�����ʱ
�ϣ���ͼ�٣�����ʱ![]() ���ɵý��ۣ�
���ɵý��ۣ�![]() .
.
��Ӧ��������Ϣ����������⣺
����![]() �ֱ���
�ֱ���![]() �ڣ���ͼ�ڣ���
�ڣ���ͼ�ڣ���![]() �⣨��ͼ�ۣ�ʱ�����������Ƿ�������������������֤��������������
�⣨��ͼ�ۣ�ʱ�����������Ƿ�������������������֤��������������![]() ��
��![]() ��
��![]() ����
����![]() ֮������������������ϵ����д����IJ��룬����Ҫ֤��.
֮������������������ϵ����д����IJ��룬����Ҫ֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���E��F�ֱ��DZ�AD��BC���е㣬����DF������E��EH��DF������ΪH��EH���ӳ��߽�DC�ڵ�G��
��1������DG��CF��������ϵ����֤����Ľ��ۣ�
��2������H��MN��CD���ֱ�AD��BC�ڵ�M��N����������ABCD�ı߳�Ϊ10����P��MN��һ�㣬���PDC�ܳ�����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ɱ߳���ȵ�С��������ɵ��������¸�ͼ�е�A��B��C��D���ڸ���ϣ�
��1����ͼ1�У�PC��PB=�� ����
��2������������̶ȵ�ֱ����ͼ�������ۼ�����д������
����ͼ2����AB���ҵ�P��ʹ��AP��PB=1��3��
����ͼ3����BC���ҵ�P��ʹ����APB�ס�DPC��
����ͼ4������ABC������һ��P������PA��PB��PC������ABC�ֳ������ȵ������֣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڵ�1��![]() �У�
�У�![]() ���ڱ�
���ڱ�![]() ����ȡһ��
����ȡһ��![]() ���ӳ�
���ӳ�![]() ��
��![]() ��ʹ
��ʹ![]() ���õ���2��
���õ���2��![]() ���ڱ�
���ڱ�![]() ����ȡһ��
����ȡһ��![]() ���ӳ�
���ӳ�![]() ��
��![]() ��ʹ
��ʹ![]() ���õ���3��
���õ���3��![]() ����������������ȥ�����
����������������ȥ�����![]() ������������
������������![]() Ϊ����ĵǶ����ǣ� ��
Ϊ����ĵǶ����ǣ� ��

A. B.
B. C.
C. D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ���ϣ�����ʦ��ʾ�����¿��е���Ŀ��

С����ͬ��С�����ۺ��������½��
��1���������̽�����ۣ��ڵȱ�������ABC�У�����EΪAB���е�ʱ����D��CB���ӳ����ϣ���ED=EC����ͼ1��ȷ���߶�AE��DB�Ĵ�С��ϵ������ֱ��д������ ��
��2�����������������Ŀ
����ʦ��������Ŀ�У�AE��DB�Ĵ�С��ϵ�ǣ� ���������£�
��ͼ2������E��EF��BC����AC�ڵ�F��(����������½�����)
��3����չ���ۣ��������
����ABC�У�AB=BC=AC=1����E��AB���ӳ����ϣ�AE=2����D��CB���ӳ����ϣ�ED=EC����ͼ3����ֱ��дCD�ij� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
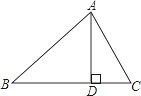
����Ŀ����ͼ����ABC�У�AD��BC��D�������������١�B+��DAC=90�㣻�ڡ�B=��DAC����![]() =
=![]() ����AB2=BDBC �� ����һ���ܹ��ж���ABC��ֱ�������ε����� ����.
����AB2=BDBC �� ����һ���ܹ��ж���ABC��ֱ�������ε����� ����.
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() ��ͼ����һ�κ���
��ͼ����һ�κ���![]() ��ͼ����
��ͼ����![]() ��
��![]() ���㣬������һ�κ����У���ʹ�߶�
���㣬������һ�κ����У���ʹ�߶�![]() ����ǣ� ��
����ǣ� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com