
����Ŀ������һԪ���η���ax2+bx+c=0��a��0������˵����ȷ���ǣ�������
����a��c��ţ���ax2+bx+c=0��a��0��һ����ʵ������
����b2��4ac��0����ax2+bx+c=0��a��0��һ�������������ʵ������
����b=a+c����ax2+bx+c=0��a��0������������ȵ�ʵ������
��������ax2+bx+c=0��a��0��������������ͬ����ô����cx2+bx+a=0��c��0������������Ҳ��ͬ��
A. ֻ���٢� B. ֻ���٢ڢ� C. ֻ���٢� D. ֻ���ڢ�
���𰸡�B
��������
����a��c��ţ������![]() ��0�������б�ʽ������ɶԢٽ����жϣ�����
��0�������б�ʽ������ɶԢٽ����жϣ�����![]() ʱ������
ʱ������![]() ��ac�����Բ���a��c�����ͬ�ţ����С���0�������б�ʽ������ɶԢڽ����жϣ�����b��a��c������
��ac�����Բ���a��c�����ͬ�ţ����С���0�������б�ʽ������ɶԢڽ����жϣ�����b��a��c������![]() ��(a ��c)2��4ac��(a��c)2��0�������б�ʽ������ɶԢ۽����жϣ�����
��(a ��c)2��4ac��(a��c)2��0�������б�ʽ������ɶԢ۽����жϣ�����![]() ����������ȵ�ʵ����������һԪ���η��̵Ķ���ɶԢܽ����ж�.
����������ȵ�ʵ����������һԪ���η��̵Ķ���ɶԢܽ����ж�.
��a��c��ţ������![]() ������
������![]() һ����ʵ���������Ԣ���ȷ����
һ����ʵ���������Ԣ���ȷ����![]() ʱ������
ʱ������![]() ��ac������a��cͬ����ţ��С���0����
��ac������a��cͬ����ţ��С���0����![]() һ�������������ʵ���������Ԣ���ȷ����b��a��c������b��4ac��(a��c)2��4ac��(a��c)2��0����һԪ���η���
һ�������������ʵ���������Ԣ���ȷ����b��a��c������b��4ac��(a��c)2��4ac��(a��c)2��0����һԪ���η���![]() ������ʵ����������һ������������ȵ�ʵ���������Ԣ۴�����
������ʵ����������һ������������ȵ�ʵ���������Ԣ۴�����
������![]() ����������ȵ�ʵ������������֪c��0,��
����������ȵ�ʵ������������֪c��0,��![]() ��ΪһԪ���η��̣����Ԣ���ȷ������Bѡ������ȷ��.
��ΪһԪ���η��̣����Ԣ���ȷ������Bѡ������ȷ��.


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�������һ�������Ϳյ���ÿ̨�����Ľ��۱�ÿ̨�յ��Ľ��۶�400Ԫ���̵���8000Ԫ������������������6400Ԫ�����յ���������ȣ�
��1����ÿ̨�������յ��Ľ��۷ֱ��Ƕ��٣�
��2����֪���������ۼ�Ϊÿ̨2100Ԫ���յ������ۼ�Ϊÿ̨1750Ԫ�����̵������������ּҵ繲100̨�����й��������x̨��33��x��40������ô���̵�Ҫ����������Ӧ��ν�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������OABC�У�OΪƽ��ֱ������ϵ��ԭ�㣬A�������Ϊ![]() ��C�������Ϊ
��C�������Ϊ![]() ����B�ڵ�һ�����ڣ���P��ԭ���������ÿ��2����λ���ȵ��ٶ�����
����B�ڵ�һ�����ڣ���P��ԭ���������ÿ��2����λ���ȵ��ٶ�����![]() ��·���ƶ�
��·���ƶ�![]() �������ų������ƶ�һ��
�������ų������ƶ�һ��![]() ��
��
![]() ���B������
���B������![]() ______
______![]()
![]() ����P�ƶ���4��ʱ�������ʱP���λ�ã��������P�����꣮
����P�ƶ���4��ʱ�������ʱP���λ�ã��������P�����꣮
![]() ���ƶ������У�����P��x�����Ϊ5����λ����ʱ�����P�ƶ���ʱ�䣮
���ƶ������У�����P��x�����Ϊ5����λ����ʱ�����P�ƶ���ʱ�䣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ�����ͼ����![]() ���ཻ��
���ཻ��![]() ��
��![]() ���㣬��
���㣬��![]() ���ཻ��
���ཻ��![]() ��,��
��,��![]() ��
��![]() �Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣬һ�κ�����ͼ�����
�Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣬һ�κ�����ͼ�����![]() ��
��![]() ��
��

![]() ��
��![]() ������ꣻ
������ꣻ
![]() ��һ�κ����ı���ʽ��
��һ�κ����ı���ʽ��
![]() ����ͼ��д��ʹһ�κ���ֵ���ڶ��κ���ֵ��
����ͼ��д��ʹһ�κ���ֵ���ڶ��κ���ֵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() ���ཻ��
���ཻ��![]() ��
��![]() ���㣬��
���㣬��![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ����
����![]() ��ֱ��
��ֱ��![]() �·���������һ�㣬����
�·���������һ�㣬����![]() ��
��![]() ���ƽ���ߣ���ֱ��
���ƽ���ߣ���ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��
![]() ��ֱ��
��ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
![]() ���߶�
���߶�![]() �ij������ʱ�����
�ij������ʱ�����![]() �����꣮
�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l1�Ľ���ʽΪ![]() ��ֱ��l2�Ľ���ʽΪ
��ֱ��l2�Ľ���ʽΪ![]() ����x�ᡢy��ֱ��ڵ�A����B��ֱ��l1��l2���ڵ�C.
����x�ᡢy��ֱ��ڵ�A����B��ֱ��l1��l2���ڵ�C.
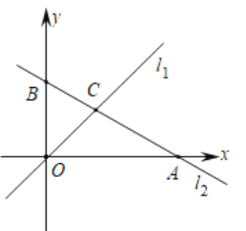

��1�����A����B����C�����꣬�������COB�������
��2����ֱ��l2�ϴ��ڵ�P������B�غϣ�������S��COP=S��COB���������P�����ꣻ
��3����y���Ҳ���һ��ֱ��ƽ����y�ᣬ�ֱ���l1��l2���ڵ�M��N���ҵ�M�ڵ�N���·���y�����Ƿ���ڵ�Q��ʹ��MNQΪ����ֱ�������Σ������ڣ���ֱ��д�����������ĵ�Q�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
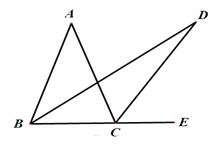
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬
�ӳ�����һ�㣬![]() ��
��![]() ��ƽ�����ཻ�ڵ�
��ƽ�����ཻ�ڵ�![]() ����
����![]() ���� ����
���� ����
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
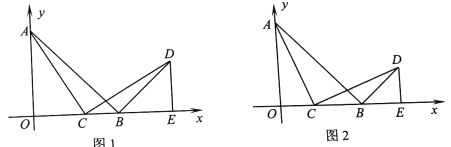
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�OA��OB����B������Ϊ(1��0)��AB��![]() ���߶�OB�ϵĶ���(��C����O��B�غ�)������AC,��AC��CD,��DE��x�ᣬ����Ϊ��E.
���߶�OB�ϵĶ���(��C����O��B�غ�)������AC,��AC��CD,��DE��x�ᣬ����Ϊ��E.
(1)��֤:��ACO����CDE;
(2)������BDE����״����֤������:
(3)��ͼ2,����BCDΪ����������ʱ�����D������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1��ʾ����Rt��ABC�У���ACB��90�㣬AC��BC����D��б��AB�ϣ���E��ֱ�DZ�BC�ϣ�����CDE��45������֤����ACD�ס�BDE��
��2����ͼ2��ʾ���ھ���ABCD�У�AB��4cm��BC��10cm����E��BC�ϣ�����AE������E��EF��AE��CD����CD���ӳ��ߣ��ڵ�F��
����BE��EC��1��9����CF�ij���
������Fǡ�����D�غϣ����ڱ���ͼ�ϻ���ͼ�Σ�����BE�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com