
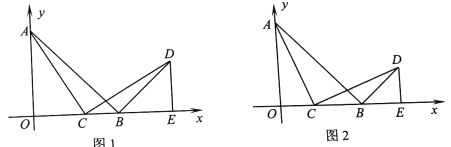
【题目】如图1,在平面直角坐标系中,OA=OB,点B的坐标为(1,0),AB=![]() ,线段OB上的动点(点C不与O、B重合),连接AC,作AC⊥CD,作DE⊥x轴,垂足为点E.
,线段OB上的动点(点C不与O、B重合),连接AC,作AC⊥CD,作DE⊥x轴,垂足为点E.
(1)求证:△ACO≌△CDE;
(2)猜想△BDE的形状,并证明结论:
(3)如图2,当△BCD为等腰三角形时,求点D的坐标.
【答案】(1)见详解;(2)等腰直角三角形;(3)(![]() ,
,![]() -1)
-1)
【解析】
(1)根据垂直的定义得到∠ACD=90°,根据余角的性质得到∠ACO=∠CDE,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到AO=CE,CO=DE,求得OB=CE,得到OC+CB=BE+CB,由等腰直角三角形的判定定理即可得到结论;
(3)设D点的纵坐标为m,当△BCD为等腰三角形时,①BC=BD,②CD=BD=![]() m,③当CD=BC>CE根据题意列方程即可得到结论.
m,③当CD=BC>CE根据题意列方程即可得到结论.
解:(1)∵AC⊥CD,
∴∠ACD=90°,
∴∠ACO+∠DCE=90°,
∵作DE⊥x轴,AO⊥OB,
∴∠DEC=∠COA=90°,
∴∠CDE+∠DCE=90°,
∴∠ACO=∠CDE,
在△ACO与△CDE中
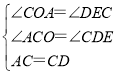
∴△ACO≌△CDE(AAS);
(2)△BDE为等腰直角三角形,
理由:∵△ACO≌△CDE,
∴AO=CE,CO=DE,
∵OA=CE,CO=DE,
∵OA=OB,
∴OB=CE,
∴OC+CB=BE+CB,
即OC=BE=DE,
∵∠DEB=90°,
∴△BDE是等腰直角三角形;
(3)解:设D点的纵坐标为m,
当△BCD为等腰三角形时,
①BC=BD,∵△BDE是等腰直角三角形,
∴DE=BE=m,
∴BD=BC=![]() m,
m,
∵CE=AO=1,
∴![]() m+m=1,
m+m=1,
∴m=![]() -1,
-1,
∴D(![]() ,
,![]() -1);
-1);
②CD=BD=![]() m,
m,
∵OC=DE=m,
∴AC=CD=![]() m,
m,
解得:m=±1(舍去),
③当CD=BC>CE(这种情况不存在0,
综上所述,当△BCD为等腰三角形时,点D的坐标(![]() ,
,![]() -1).
-1).


科目:初中数学 来源: 题型:
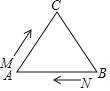
【题目】如图,![]() 中,
中,![]() ,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为
,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为![]() ,点N的速度为
,点N的速度为![]() 当点N第一次到达B点时,M、N同时停止运动.
当点N第一次到达B点时,M、N同时停止运动.
![]() 点M,N运动几秒后,M、N两点重合?
点M,N运动几秒后,M、N两点重合?
![]() 点M、N运动几秒后,可得到等边三角形
点M、N运动几秒后,可得到等边三角形![]() ?
?
![]() 当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.
当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一元二次方程ax2+bx+c=0(a≠0)下列说法正确的是( )
①若a,c异号,则方程ax2+bx+c=0(a≠0)一定有实数根;
②若b2﹣4ac>0,则方程ax2+bx+c=0(a≠0)一定有两个不相等实数根;
③若b=a+c,则方程ax2+bx+c=0(a≠0)有两个不相等的实数根;
④若方程ax2+bx+c=0(a≠0)的两根符号相同,那么方程cx2+bx+a=0(c≠0)的两根符号也相同.
A. 只有①③ B. 只有①②④ C. 只有①② D. 只有②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图

(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() 、
、![]() 两枚均匀的小立方体(立方体的每个面上分别标有数字
两枚均匀的小立方体(立方体的每个面上分别标有数字![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ).用小明掷
).用小明掷![]() 立方体朝上的数字为
立方体朝上的数字为![]() ,小明掷
,小明掷![]() 立方体朝上的数字为
立方体朝上的数字为![]() 来确定点
来确定点![]() ,则小明各掷一次所确定的点
,则小明各掷一次所确定的点![]() 落在已知抛物线
落在已知抛物线![]() 上的概率是________.
上的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 所在平面内一点,过点
所在平面内一点,过点![]() 分别作
分别作![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.

若点![]() 在
在![]() 上(如图①),此时
上(如图①),此时![]() ,可得结论:
,可得结论:![]() .
.
请应用上述信息解决下列问题:
当点![]() 分别在
分别在![]() 内(如图②),
内(如图②),![]() 外(如图③)时,上述结论是否成立?若成立,请给予证明;若不成立,
外(如图③)时,上述结论是否成立?若成立,请给予证明;若不成立,![]() ,
,![]() ,
,![]() ,与
,与![]() 之间又有怎样的数量关系,请写出你的猜想,不需要证明.
之间又有怎样的数量关系,请写出你的猜想,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论;
(2)过点H作MN∥CD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点,求△PDC周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
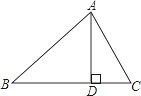
【题目】如图,△ABC中,AD⊥BC于D,下列条件:①∠B+∠DAC=90°;②∠B=∠DAC;③![]() =
=![]() ;④AB2=BDBC . 其中一定能够判定△ABC是直角三角形的有( )个.
;④AB2=BDBC . 其中一定能够判定△ABC是直角三角形的有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com