
【题目】现有![]() 、
、![]() 两枚均匀的小立方体(立方体的每个面上分别标有数字
两枚均匀的小立方体(立方体的每个面上分别标有数字![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ).用小明掷
).用小明掷![]() 立方体朝上的数字为
立方体朝上的数字为![]() ,小明掷
,小明掷![]() 立方体朝上的数字为
立方体朝上的数字为![]() 来确定点
来确定点![]() ,则小明各掷一次所确定的点
,则小明各掷一次所确定的点![]() 落在已知抛物线
落在已知抛物线![]() 上的概率是________.
上的概率是________.
【答案】![]()
【解析】
列举出所有情况,看所求的情况占总情况的多少即可.
列表得:
(1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
(1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
(1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
(1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
(1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
(1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
两个立方体上都有6个数字,那么共有6×6=36种情况,
可在抛物线上的有(1,2),(2,1),(3,2),(4,5)共4种情况,
那么点P落在已知抛物线y=x24x+5上的概率是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300![]() 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),

(1)求围栏的长和宽;
(2)能否围成面积为400 ![]() 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1的解析式为![]() ,直线l2的解析式为
,直线l2的解析式为![]() ,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
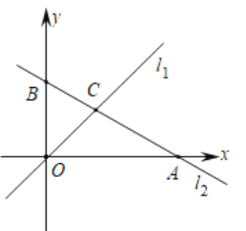

(1)求点A、点B、点C的坐标,并求出△COB的面积;
(2)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,请求出点P的坐标;
(3)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)画出△ABC和△A1B1C1关于原点O对称,画出△A1B1C1,并写出△A1B1C1的各顶点的坐标;
(2)将△ABC绕着点O按顺时针方向旋转90°得到的△A2B2C2,画出△A2B2C2,并写出△A2B2C2的各顶点的坐标.
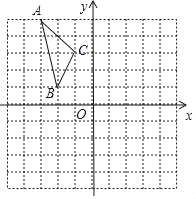
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,OA=OB,点B的坐标为(1,0),AB=![]() ,线段OB上的动点(点C不与O、B重合),连接AC,作AC⊥CD,作DE⊥x轴,垂足为点E.
,线段OB上的动点(点C不与O、B重合),连接AC,作AC⊥CD,作DE⊥x轴,垂足为点E.
(1)求证:△ACO≌△CDE;
(2)猜想△BDE的形状,并证明结论:
(3)如图2,当△BCD为等腰三角形时,求点D的坐标.
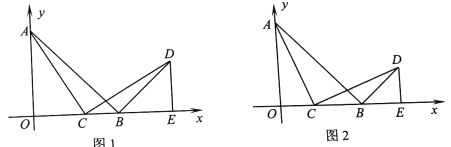
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果为“A.非常了解”、“B.了解”、“C.基本了解”三个等级,并根据调查结果制作了如下两幅不完整的统计图.
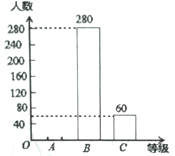
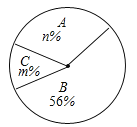
(1)这次调查的市民人数为_____人,m=______,n=_______;
(2)补全条形统计图;
(3)若该市约有市民1200000人,请你根据抽样调查的结果,估计该市对“社会主义核心价值观”达到“A.非常了解”程度的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,已知△ABC中,AC=BC=AB=6,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的距离为整数的点有( )个.
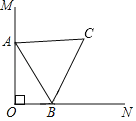
A.5B.6C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点F是![]() ABCD的边AD上的三等分点,BF交AC于点E,如果△AEF的面积为2,那么四边形CDFE的面积等于( )
ABCD的边AD上的三等分点,BF交AC于点E,如果△AEF的面积为2,那么四边形CDFE的面积等于( )

A. 18 B. 22 C. 24 D. 46
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E为BC中点连接AE,DF⊥AE于点F,连接CF,FG⊥CF交AD于点G,下列结论:①CF=CD;②G为AD中点;③△DCF∽△AGF;④![]() ,其中结论正确的个数有( )
,其中结论正确的个数有( )
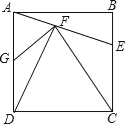
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com