练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，反比例函数的图象与一次函数的图象交于、两点，则下列一次函数中，能使线段最长的是（ ）

    A. B. C. D.

    【答案】D

    【解析】

    分别求出反比例函数与一次函数所形成的交点A、B的坐标，再利用两点之间的距离公式求出AB的长，进行比较即可．

    解方程组

    y＝，y＝x+4，得

    x＝2+2，y＝2+2或x＝22，y＝22，

    可知A点坐标是（-2+2，2+2），B点坐标是（-2-2，2-2），

    ∴AB===8；

    同理可求函数y=与y=x的交点之间的距离==4；

    同理可求函数y=与y=x-3的交点之间的距离==5；

    同理可求函数y=与y=x-5的交点之间的距离=；

    ∵＞＞＞，

    ∴函数y=与y=x-5相交形成的两点A、B之间的距离最长．

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）如图1所示，在Rt△ABC中，∠ACB＝90°，AC＝BC，点D在斜边AB上，点E在直角边BC上，若∠CDE＝45°，求证：△ACD∽△BDE．

    （2）如图2所示，在矩形ABCD中，AB＝4cm，BC＝10cm，点E在BC上，连接AE，过点E作EF⊥AE交CD（或CD的延长线）于点F．

    ①若BE：EC＝1：9，求CF的长；

    ②若点F恰好与点D重合，请在备用图上画出图形，并求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中，P为AB边上一点，将△BCP沿CP折叠，得到△FCP．

    （1）如图1，延长PF交AD于E，求证：EF=ED；

    （2）如图2，DF，CP的延长线交于点G，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，tan∠ACB=2，D在△ABC内部，且AD=CD，∠ADC=90°，连接BD，若△BCD的面积为10，则AD的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB=AC=AD，∠CAD=60°，分别连接BC、BD，作AE平分∠BAC交BD于点E，若BE=4，ED=8，则DF=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点D、E在BC边上，点F在AC边上，将△ABD沿着AD翻折，使点B和点E重合，将△CEF沿着EF翻折，点C恰与点A重合．结论：①∠BAC=90°，②DE=EF，③∠B=2∠C，④AB=EC，正确的有（　　）

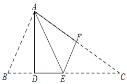
    A.①②③④B.③④C.①②④D.①②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市制米厂接到加工大米任务，要求5天内加工完220吨大米，制米厂安排甲、乙两车间共同完成加工任务，乙车间加工中途停工一段时间维修设备，然后改变加工效率继续加工，直到与甲车间同时完成加工任务为止．设甲、乙两车间各自加工大米数量y（吨）与甲车间加工时间s（天）之间的关系如图（1）所示；未加工大米w（吨）与甲加工时间x（天）之间的关系如图（2）所示，请结合图象回答下列问题：

    （1）甲车间每天加工大米　 　吨，a=　 　．

    （2）求乙车间维修设备后，乙车间加工大米数量y（吨）与x（天）之间函数关系式．

    （3）若55吨大米恰好装满一节车厢，那么加工多长时间装满第一节车厢？再加工多长时间恰好装满第二节车厢？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学兴趣活动课上，小明将等腰△ABC的底边BC与直线1重合，问：

    （1）已知AB＝AC＝6，∠BAC＝120°，点P在BC边所在的直线l上移动，根据“直线外一点到直线上所有点的连线中垂线段最短”，小明发现AP的最小值是　 　；

    （2）为进一步运用该结论，小明发现当AP最短时，在Rt△ABP中，∠P＝90°，作了AD平分∠BAP，交BP于点D，点E、F分别是AD、AP边上的动点，连接PE、EF，小明尝试探索PE+EF的最小值，为转化EF，小明在AB上截取AN，使得AN＝AF，连接NE，易证△AEF≌△AEN，从而将PE+EF转化为PE+EN，转化到（1）的情况，若BP＝3，AB＝6，AP＝3，则PE+EF的最小值为　 　；

    （3）请应用以上转化思想解决问题（3），在直角△ABC中，∠C＝90°，∠B＝30°，AC＝10，点D是CD边上的动点，连接AD，将线段AD顺时针旋转60°，得到线段AP，连接CP，求线段CP的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P是斜边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,EF与AP相交于点O,则OF的最小值为 ( )

    A. 4.8 B. 1.2

    C. 3.6 D. 2.4

    查看答案和解析>>

    同步练习册答案