
【题目】在正方形ABCD中,P为AB边上一点,将△BCP沿CP折叠,得到△FCP.
(1)如图1,延长PF交AD于E,求证:EF=ED;
(2)如图2,DF,CP的延长线交于点G,求![]() 的值.
的值.

【答案】(1)证明见解析(2)![]()
【解析】
(1)连接CE,通过全等三角形的判定,得到Rt△CFE≌Rt△CDE,进而得出结论;
(2)连接BG、BF、BD,作CH⊥DF,垂足为H.依据△CFG≌△CBG,可得GF=GB,进而得出△GBF是等腰直角三角形,故BF=![]() BG.再判定△BGA∽△FBD,即可得到
BG.再判定△BGA∽△FBD,即可得到![]() .
.
(1)如图1,连接CE,
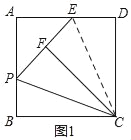
∵四边形ABCD是正方形,
∴BC=CD,∠B=∠D=90°.
∵△PBC和△FPC关于PC对称,
∴BC=CF,∠B=∠PFC=90°.
∴∠EFC=90°.
∴∠EFC=∠D=90°,CF=CD.
∵CE=CE,
∴Rt△EFC≌Rt△DFC(HL).
∴EF=ED.
(2)如图2,连接BG、BF、BD,作CH⊥DF,垂足为H.
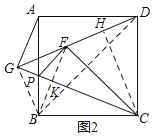
∵四边形ABCD是正方形,
∴BC=CD.
∵CH⊥DF,
∴∠HCF=![]() ,
,
∵△PBC和△FPC关于PC对称,
∴BC=CF,∠FCG=∠BCG.
∴EB⊥CG.
又∵CG=CG,
∴△CFG≌△CBG.
∴GF=GB.
∵∠HCF=![]() ,∠FCG=∠BCG=
,∠FCG=∠BCG=![]() ,
,
∴∠HCK=![]() =45°.
=45°.
∴∠PFH=135°.
∴∠GFB=45°.
∴∠GBF=45°.
∴△GBF是等腰直角三角形.
∴![]() .
.
∵∠ABD=45°,
∴∠GBA=∠FBD.
∵![]() ,
,
∴△BGA∽△FBD.
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 所在平面内一点,过点
所在平面内一点,过点![]() 分别作
分别作![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.

若点![]() 在
在![]() 上(如图①),此时
上(如图①),此时![]() ,可得结论:
,可得结论:![]() .
.
请应用上述信息解决下列问题:
当点![]() 分别在
分别在![]() 内(如图②),
内(如图②),![]() 外(如图③)时,上述结论是否成立?若成立,请给予证明;若不成立,
外(如图③)时,上述结论是否成立?若成立,请给予证明;若不成立,![]() ,
,![]() ,
,![]() ,与
,与![]() 之间又有怎样的数量关系,请写出你的猜想,不需要证明.
之间又有怎样的数量关系,请写出你的猜想,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,王老师出示了如下框中的题目.

小明与同桌小聪讨论后,进行了如下解答:
(1)特殊情况探索结论:在等边三角形ABC中,当点E为AB的中点时,点D在CB点延长线上,且ED=EC;如图1,确定线段AE与DB的大小关系.请你直接写出结论 ;
(2)特例启发,解答题目
王老师给出的题目中,AE与DB的大小关系是: .理由如下:
如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题
在△ABC中,AB=BC=AC=1;点E在AB的延长线上,AE=2;点D在CB的延长线上,ED=EC,如图3,请直接写CD的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于D,下列条件:①∠B+∠DAC=90°;②∠B=∠DAC;③![]() =
=![]() ;④AB2=BDBC . 其中一定能够判定△ABC是直角三角形的有( )个.
;④AB2=BDBC . 其中一定能够判定△ABC是直角三角形的有( )个.
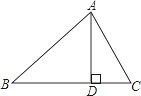
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分別交AB、BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为____________°

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新能源汽车环保节能,越来越受到消费者的喜爱.各种品牌相继投放市场.一汽贸公司经销某品牌新能源汽车.去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元.销售数量与去年一整年的相同.销售总额比去年一整年的少20%,今年1~5月份每辆车的销售价格是多少万元?设今年1~5月份每辆车的销售价格为x万元.根据题意,列方程正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校利用暑假进行田径场的改造维修,项目承包单位派遣一号施工队进场施工,计划用40天时间完成整个工程:当一号施工队工作5天后,承包单位接到通知,有一大型活动要在该田径场举行,要求比原计划提前14天完成整个工程,于是承包单位派遣二号与一号施工队共同完成剩余工程,结果按通知要求如期完成整个工程.
(1)若二号施工队单独施工,完成整个工程需要多少天?
(2)若此项工程一号、二号施工队同时进场施工,完成整个工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:EC,⑤OD2=DECD,正确的有( )

A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com