
【题目】如图,已知△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分別交AB、BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为____________°

【答案】115°
【解析】
根据三角形的内角和得到∠BAC+∠ACB=130°,根据线段的垂直平分线的性质得到AM=PM,PN=CN,由等腰三角形的性质得到∠MAP=∠APM,∠CPN=∠PCN,推出∠MAP+∠PCN=∠PAC+∠ACP=![]() ×130°=65°,于是得到结论.
×130°=65°,于是得到结论.
∵∠ABC=50°,
∴∠BAC+∠ACB=130°,
∵若M在PA的中垂线上,N在PC的中垂线上,
∴AM=PM,PN=CN,
∴∠MAP=∠APM,∠CPN=∠PCN,
∵∠APC=180°-∠APM-∠CPN=180°-∠PAC-∠ACP,
∴∠MAP+∠PCN=∠PAC+∠ACP=![]() ×130°=65°,
×130°=65°,
∴∠APC=115°,
故答案为:115°


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】为考察两名实习工人的工作情况,质检部将他们工作某一周每天生产合格产品的个数整理成甲、乙两组数据,如下表:
甲 | 2 | 6 | 7 | 7 | 8 |
乙 | 2 | 4 | 5 | 8 | 8 |
根据以上数据,下面说法正确的是( )
A.甲、乙的众数相同B.甲、乙的中位数相同
C.甲的平均数小于乙的平均数D.甲的方差小于乙的方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90 ,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
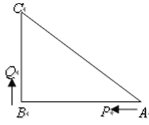
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,AD⊥BC,点D为垂足,AD=BD,点E在AD上,BE=AC
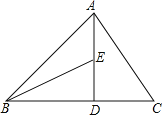
(1)求证:△BDE≌△ADC
(2)若M、N分别是BE、AC的中点,分别联结DM、DN. 求证:DM⊥DN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:

(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,P为AB边上一点,将△BCP沿CP折叠,得到△FCP.
(1)如图1,延长PF交AD于E,求证:EF=ED;
(2)如图2,DF,CP的延长线交于点G,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙为两座建筑物,它们之间的水平距离BC为30日,在A点测得D点的仰角∠EAD=45°,在B点测得D点的仰角为∠CBD=60°,测得甲、乙这两座建筑物的高度分别为( )米.

A. 10![]() ,30 B. 30,30
,30 B. 30,30![]() C. 30
C. 30![]() ﹣3,30 D. 30
﹣3,30 D. 30![]() ﹣30,30
﹣30,30![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC=AD,∠CAD=60°,分别连接BC、BD,作AE平分∠BAC交BD于点E,若BE=4,ED=8,则DF=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车的背面,有一种特殊形状的刮雨器,忽略刮雨器的宽度可抽象为一条折线![]() ,如图
,如图![]() 所示,量得连杆
所示,量得连杆![]() 长为
长为![]() ,雨刮杆
,雨刮杆![]() 长为
长为![]() ,
,![]() .若启动一次刮雨器,雨刮杆
.若启动一次刮雨器,雨刮杆![]() 正好扫到水平线
正好扫到水平线![]() 的位置,如图
的位置,如图![]() 所示.
所示.

![]() 求雨刮杆
求雨刮杆![]() 旋转的最大角度及
旋转的最大角度及![]() 、
、![]() 两点之间的距离;
两点之间的距离;
![]() 求雨刮杆
求雨刮杆![]() 扫过的最大面积.
扫过的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com