
【题目】已知:如图,△ABC中,AD⊥BC,点D为垂足,AD=BD,点E在AD上,BE=AC
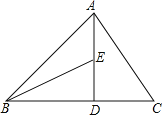
(1)求证:△BDE≌△ADC
(2)若M、N分别是BE、AC的中点,分别联结DM、DN. 求证:DM⊥DN
【答案】(1)见解析;(2)见解析
【解析】
(1)运用HL证明△BDE≌△ADC即可;
(2)由△BDE≌△ADC可得DE=DC,∠DEM=∠C,BE=AC,再依据M、N分别是BE、AC的中点,从而可得CN=EM,进而可证明△DEM≌△DCN,可得∠CDN=∠EDM,结合∠ADC=90°即可证得结论.
(1)∵AD⊥BC,
∴∠ADC=∠BDE=90°,
在Rt△ADC和Rt△BDE中,
![]()
∴△BDE≌△ADC;
(2)如图,
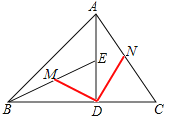
∵△BDE≌△ADC,
∴DE=DC,∠DEM=∠C,
∵M、N分别是BE、AC的中点且BE=AC,
∴EM=CN,
在△DEM和△DCN中,
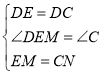
∴△DEM≌△DCN
∴∠EDM=∠CDN
∵∠CDN+∠NDA=90°,
∴∠MDA+∠NDA=90°,
即DM⊥DN.


 同步轻松练习系列答案
同步轻松练习系列答案科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图

(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由边长相等的小正方形组成的网格,以下各图中点A、B、C、D都在格点上.
(1)在图1中,PC:PB= ;
(2)利用网格和无刻度的直尺作图,保留痕迹,不写作法.
①如图2,在AB上找点P,使得AP:PB=1:3;
②如图3,在BC上找点P,使得△APB∽△DPC;
③如图4,在△ABC中内找一点P,连接PA、PB、PC,将△ABC分成面积相等的三部分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,王老师出示了如下框中的题目.

小明与同桌小聪讨论后,进行了如下解答:
(1)特殊情况探索结论:在等边三角形ABC中,当点E为AB的中点时,点D在CB点延长线上,且ED=EC;如图1,确定线段AE与DB的大小关系.请你直接写出结论 ;
(2)特例启发,解答题目
王老师给出的题目中,AE与DB的大小关系是: .理由如下:
如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题
在△ABC中,AB=BC=AC=1;点E在AB的延长线上,AE=2;点D在CB的延长线上,ED=EC,如图3,请直接写CD的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于D,下列条件:①∠B+∠DAC=90°;②∠B=∠DAC;③![]() =
=![]() ;④AB2=BDBC . 其中一定能够判定△ABC是直角三角形的有( )个.
;④AB2=BDBC . 其中一定能够判定△ABC是直角三角形的有( )个.
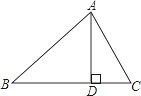
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分別交AB、BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为____________°

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校利用暑假进行田径场的改造维修,项目承包单位派遣一号施工队进场施工,计划用40天时间完成整个工程:当一号施工队工作5天后,承包单位接到通知,有一大型活动要在该田径场举行,要求比原计划提前14天完成整个工程,于是承包单位派遣二号与一号施工队共同完成剩余工程,结果按通知要求如期完成整个工程.
(1)若二号施工队单独施工,完成整个工程需要多少天?
(2)若此项工程一号、二号施工队同时进场施工,完成整个工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_______秒时,△BCA与点P、N、B为顶点的三角形全等.(2个全等三角形不重合)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com