
【题目】数学兴趣活动课上,小明将等腰△ABC的底边BC与直线1重合,问:
(1)已知AB=AC=6,∠BAC=120°,点P在BC边所在的直线l上移动,根据“直线外一点到直线上所有点的连线中垂线段最短”,小明发现AP的最小值是 ;
(2)为进一步运用该结论,小明发现当AP最短时,在Rt△ABP中,∠P=90°,作了AD平分∠BAP,交BP于点D,点E、F分别是AD、AP边上的动点,连接PE、EF,小明尝试探索PE+EF的最小值,为转化EF,小明在AB上截取AN,使得AN=AF,连接NE,易证△AEF≌△AEN,从而将PE+EF转化为PE+EN,转化到(1)的情况,若BP=3![]() ,AB=6,AP=3,则PE+EF的最小值为 ;
,AB=6,AP=3,则PE+EF的最小值为 ;
(3)请应用以上转化思想解决问题(3),在直角△ABC中,∠C=90°,∠B=30°,AC=10,点D是CD边上的动点,连接AD,将线段AD顺时针旋转60°,得到线段AP,连接CP,求线段CP的最小值.

【答案】(1)3;(2)![]() ;(3)PC的最小值为5.
;(3)PC的最小值为5.
【解析】
(1)如图1中,作AH⊥BC于H.根据垂线段最短,求出AH即可解决问题.
(2)如图2中,在AB上截取AN,使得AN=AF,连接NE.作PH⊥AB于H.由△EAN≌△EAF(SAS),推出EN=EF,推出PE+EF=PE+NE,推出当P,E,N共线且与PH重合时,PE+PF的值最小,最小值为线段PH的长.
(3)如图3中,在AB上取一点K,使得AK=AC,连接CK,DK.由△PAC≌△DAK(SAS),推出PC=DK,易知KD⊥BC时,KD的值最小,求出KD的最小值即可解决问题.
解:(1)如图1中,作AH⊥BC于H.
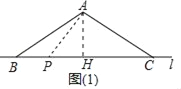
∵AB=AC=6,AH⊥BC,
∴∠BAH=∠CAH=![]() ∠BAC=60°,
∠BAC=60°,
∴AH=ABcos60°=3,
根据垂线段最短可知,当AP与AH重合时,PA的值最小,最小值为3.
故答案为3.
(2)如图2中,在AB上截取AN,使得AN=AF,连接NE.作PH⊥AB于H.
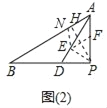
∵∠EAN=∠EAF,AN=AF,AE=AE,
∴△EAN≌△EAF(SAS),
∴EN=EF,
∴PE+EF=PE+NE,
∴当P,E,N共线且与PH重合时,PE+PF的值最小,最小值为线段PH的长,
∵![]() ABPH=
ABPH=![]() PAPB,
PAPB,
∴PH=![]() =
=![]() ,
,
∴PE+EF的最小值为![]() .
.
故答案为![]() .
.
(3)如图3中,在AB上取一点K,使得AK=AC,连接CK,DK.
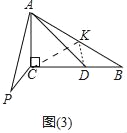
∵∠ACB=90°,∠B=30°,
∴∠CAK=60°,
∴∠PAD=∠CAK,
∴∠PAC=∠DAK,
∵PA=DA,CA=KA,
∴△PAC≌△DAK(SAS),
∴PC=DK
∵KD⊥BC时,KD的值最小,最小值为5,
∴PC的最小值为5.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】本学期学习了一元一次不等式的解法,下面是甲同学的解题过程:
解不等式![]() .
.
解:不等式两边同时乘以4,得:![]()
去分母,得:![]()
去括号,得:![]()
移项,得:![]()
合并同类项,得:![]()
系数化1,得:![]()
不等式的解集在数轴上表示为:
![]()
上述甲同学的解题过程从第___步开始出现错误,错误的原因是____.请帮甲同学改正错误,写出完整的解题过程,并把正确解集在数轴上表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的号召,学校开设了足球兴趣拓展班,计划同时购买A,B两种足球30个,A,B两种足球的价格分别为50元![]() 个,80元
个,80元![]() 个,设购买B种足球x个,购买两种足球的总费用为y元.
个,设购买B种足球x个,购买两种足球的总费用为y元.
![]() 求y关于x的函数表达式.
求y关于x的函数表达式.
![]() 在总费用不超过1600元的前提下,从节省费用的角度来考虑,求总费用的最小值.
在总费用不超过1600元的前提下,从节省费用的角度来考虑,求总费用的最小值.
![]() 因足球兴趣拓展班的人数增多,所以实际购买中这两种足球总数超过30个,总费用为2000元,则该学校可能共购买足球______个
因足球兴趣拓展班的人数增多,所以实际购买中这两种足球总数超过30个,总费用为2000元,则该学校可能共购买足球______个![]() 直接写出答案
直接写出答案![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运动服装店销售某品牌S号,M号,L号,XL号,XXL号五种不同型号服装,随机统计该品牌运动服装一周的销售情况并绘制如图所示不完整统计图.
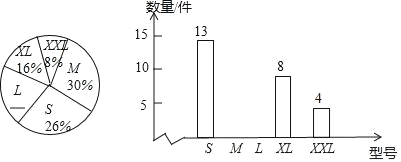
(1)L号运动服一周的销售所占百分比为 .
(2)请补全条形统计图;
(3)服装店老板打算再次购进该品牌服饰共600件,根据各种型号的销售情况,你认为购进XL号约多少件比较合适,请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=40°,点D在BC边上(不与C、D点重合),点P、点Q分别是AC、AB边上的动点,当△DPQ的周长最小时,则∠PDQ的度数为( )

A. 140°B. 120°C. 100°D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,⊙O过BC的中点D,且DE垂直AC于E.
(1)求证:AB=AC;
(2)求证:DE是⊙O的切线;
(3)若AB=13,BC=10,求DE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.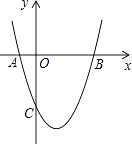
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有除颜色外都相同的球,其中红球5个,白球7个、黑球12个.
(1)求从袋中摸一个球是白球的概率;
(2)现从袋中取出若干个红球,放入相同数量的黑球,使从袋中摸出一个球是黑球的概率不超过60%,问至多取出多少个红球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种电子产品共 ![]() 件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为
件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为 ![]() .
.
(1)该批产品有正品件;
(2)如果从中任意取出 ![]() 件,利用列表或树状图求取出
件,利用列表或树状图求取出 ![]() 件都是正品的概率.
件都是正品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com