练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某种电子产品共 件，其中有正品和次品．已知从中任意取出一件，取得的产品为次品的概率为 ．
    （1）该批产品有正品件；
    （2）如果从中任意取出 件，利用列表或树状图求取出 件都是正品的概率．

    【答案】
    （1）3
    （2）解：画树状图得：

    ∵结果共有12种情况，且各种情况都是等可能的，其中两次取出的都是正品共6种，

    ∴P（两次取出的都是正品）= ．


    【解析】（1）∵某种电子产品共4件，从中任意取出一件，取得的产品为次品的概率为 ；

    ∴该批产品有正品为：4﹣4× =3．

    故答案为：3；

    （1）根据概率公式，得到该批产品的正品数值；（2）根据画树状图，得到结果共有12种情况，且各种情况都是等可能的，其中两次取出的都是正品共6种，求出取出 2 件都是正品的概率．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】数学兴趣活动课上，小明将等腰△ABC的底边BC与直线1重合，问：

    （1）已知AB＝AC＝6，∠BAC＝120°，点P在BC边所在的直线l上移动，根据“直线外一点到直线上所有点的连线中垂线段最短”，小明发现AP的最小值是　 　；

    （2）为进一步运用该结论，小明发现当AP最短时，在Rt△ABP中，∠P＝90°，作了AD平分∠BAP，交BP于点D，点E、F分别是AD、AP边上的动点，连接PE、EF，小明尝试探索PE+EF的最小值，为转化EF，小明在AB上截取AN，使得AN＝AF，连接NE，易证△AEF≌△AEN，从而将PE+EF转化为PE+EN，转化到（1）的情况，若BP＝3，AB＝6，AP＝3，则PE+EF的最小值为　 　；

    （3）请应用以上转化思想解决问题（3），在直角△ABC中，∠C＝90°，∠B＝30°，AC＝10，点D是CD边上的动点，连接AD，将线段AD顺时针旋转60°，得到线段AP，连接CP，求线段CP的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】玲玲家准备装修一套新住房，若甲、乙两个装饰公司合作，需6周完成，共需装修费为5.2万元；若甲公司单独做4周后，剩下的由乙公司来做，还需9周才能完成，共需装修费4.8万元.玲玲的爸爸妈妈商量后决定只选一个公司单独完成.

    （1）如果从节约时间的角度考虑应选哪家公司？

    （2）如果从节约开支的角度考虑呢？请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇，下表是近两周的销售情况：

    销售时段

    销售数量

    销售收入

    A种型号

    B种型号

    第一周

    3台

    5台

    1800元

    第二周

    4台

    10台

    3100元

    （进价、售价均保持不变，利润=销售收入-进货成本）

    （1）求A、B两种型号的电风扇的销售单价；

    （2）若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台，求A种型号的电风扇最多能采购多少台？

    （3）在（2）的条件下，超市销售完这30台电风扇能否实现利润为1400元的目标？若能，请给出相应的采购方案；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在结束了380课时初中阶段教学内容的教学后，王老师计划按原课程设置再增加70课时用于总复习，将380课时按内容所占比例，绘制如下统计图表（图1、图2），请根据图表提供的信息，回答问题：

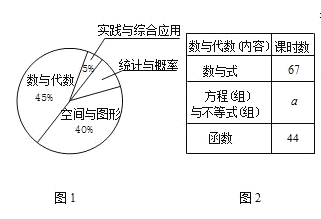
    （1）图1中“统计与概率”所在扇形的圆心角为　 　度；

    （2）图2中的a＝　 　；

    （3）在70课时的总复习中，王老师应安排多少课时复习图形与几何内容？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是一块长、宽、高分别为6cm、4cm、3cm的长方体木块，一只蚂蚁要从长方体木块的一个顶点A处，沿着长方体的表面到长方体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是（ ）

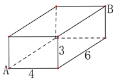
    A. cm B. cm C. cm D. 9cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对非负实数x“四舍五入”到个位的值记为<x>，即当n为非负整数时，若，则<x>＝n，如<0.46>=0，<3.67>=4。给出下列关于<x>的结论：

    ①<1.493>=1；

    ②<2x>=2<x>；

    ③若，则实数x的取值范围是；

    ④当x≥0，m为非负整数时，有；

    ⑤。

    其中，正确的结论有 　（填写所有正确的序号）。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在□ABCD中，点E是边CD的中点，连接BE并延长，交AD延长线于点F，连接BD、CF.

    （1）求证：△CEB≌△DEF；

    （2）若AB=BF，试判断四边形BCFD的形状，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将平行四边形纸片ABCD按如图方式折叠，使点C与A重合，点D落到D′处，折痕为EF．

    （1）求证：△ABE≌△AD′F；

    （2）连接CF，判断四边形AECF是什么特殊四边形？证明你的结论．

    查看答案和解析>>

    同步练习册答案