
°æƒø°øŒ™¡ÀœÏ”¶°∞◊„«ÚΩ¯–£‘∞°±µƒ∫≈’Ÿ£¨—ß–£ø™…Ë¡À◊„«Ú–À»§Õÿ’π∞ý£¨º∆ªÆÕ¨ ±π∫¬ÚA£¨B¡Ω÷÷◊„«Ú30∏ˆ£¨A£¨B¡Ω÷÷◊„«Úµƒº€∏Ò∑÷±Œ™50‘™![]() ∏ˆ£¨80‘™
∏ˆ£¨80‘™![]() ∏ˆ£¨…Ëπ∫¬ÚB÷÷◊„«Úx∏ˆ£¨π∫¬Ú¡Ω÷÷◊„«Úµƒ◊Ð∑—”√Œ™y‘™£Æ
∏ˆ£¨…Ëπ∫¬ÚB÷÷◊„«Úx∏ˆ£¨π∫¬Ú¡Ω÷÷◊„«Úµƒ◊Ð∑—”√Œ™y‘™£Æ
![]() «Ûyπÿ”⁄xµƒ∫Ø ˝±Ì¥Ô Ω£Æ
«Ûyπÿ”⁄xµƒ∫Ø ˝±Ì¥Ô Ω£Æ
![]() ‘⁄◊Ð∑—”√≤ª≥¨π˝1600‘™µƒ«∞÷œ¬£¨¥”Ω⁄ °∑—”√µƒΩ«∂»¿¥øº¬«£¨«Û◊Ð∑—”√µƒ◊Ó–°÷µ£Æ
‘⁄◊Ð∑—”√≤ª≥¨π˝1600‘™µƒ«∞÷œ¬£¨¥”Ω⁄ °∑—”√µƒΩ«∂»¿¥øº¬«£¨«Û◊Ð∑—”√µƒ◊Ó–°÷µ£Æ
![]() “Ú◊„«Ú–À»§Õÿ’π∞ýµƒ»À ˝‘ˆ∂ý£¨À˘“‘ µº π∫¬Ú÷–’‚¡Ω÷÷◊„«Ú◊Ð ˝≥¨π˝30∏ˆ£¨◊Ð∑—”√Œ™2000‘™£¨‘Ú∏√—ß–£ø…ƒÐπ≤π∫¬Ú◊„«Ú______∏ˆ
“Ú◊„«Ú–À»§Õÿ’π∞ýµƒ»À ˝‘ˆ∂ý£¨À˘“‘ µº π∫¬Ú÷–’‚¡Ω÷÷◊„«Ú◊Ð ˝≥¨π˝30∏ˆ£¨◊Ð∑—”√Œ™2000‘™£¨‘Ú∏√—ß–£ø…ƒÐπ≤π∫¬Ú◊„«Ú______∏ˆ![]() ÷±Ω”–¥≥ˆ¥∞∏
÷±Ω”–¥≥ˆ¥∞∏![]()
°æ¥∞∏°ø£®1£©![]() £ª£®2£©
£ª£®2£©![]() ‘™£ª£®3£©31£¨34£¨37
‘™£ª£®3£©31£¨34£¨37
°æΩ‚Œˆ°ø
![]() ∏˘æð◊Ð∑—”√
∏˘æð◊Ð∑—”√![]() ◊„«Ú∑—”√
◊„«Ú∑—”√![]() ◊„«Ú∑—”√¡–≥ˆΩ‚Œˆ Ωº¥ø…£ª
◊„«Ú∑—”√¡–≥ˆΩ‚Œˆ Ωº¥ø…£ª
![]() œ»∏˘æð◊„«Ú◊Ð ˝30∏ˆ∫Õ◊Ð∑—”√≤ª≥¨π˝1600«Û≥ˆxµƒ»°÷µ∑∂Œß£¨‘Ÿ∏˘æ𓪥Œ∫Ø ˝µƒ‘ˆºı–‘«Û≥ˆ◊Ð∑—”√◊Ó–°÷µ£ª
œ»∏˘æð◊„«Ú◊Ð ˝30∏ˆ∫Õ◊Ð∑—”√≤ª≥¨π˝1600«Û≥ˆxµƒ»°÷µ∑∂Œß£¨‘Ÿ∏˘æ𓪥Œ∫Ø ˝µƒ‘ˆºı–‘«Û≥ˆ◊Ð∑—”√◊Ó–°÷µ£ª
![]() …ËA◊„«Úπ∫¬Úm∏ˆ£¨B◊„«Úπ∫¬Ún∏ˆ£¨∏˘æð◊Ð∑—”√Œ™2000‘™¡–≥ˆ∑Ω≥Ã
…ËA◊„«Úπ∫¬Úm∏ˆ£¨B◊„«Úπ∫¬Ún∏ˆ£¨∏˘æð◊Ð∑—”√Œ™2000‘™¡–≥ˆ∑Ω≥Ã![]() £¨µ√µΩ
£¨µ√µΩ![]() £¨‘Ÿ∂‘nµƒ÷µΩ¯––∑÷¿ýÃ÷¬€£¨«Û≥ˆ¬˙◊„
£¨‘Ÿ∂‘nµƒ÷µΩ¯––∑÷¿ýÃ÷¬€£¨«Û≥ˆ¬˙◊„![]() µƒ’˚ ˝Ω‚£¨º¥ø…µ√µΩ◊Ð«Ú ˝£Æ
µƒ’˚ ˝Ω‚£¨º¥ø…µ√µΩ◊Ð«Ú ˝£Æ
Ω‚£∫![]() £¨º¥
£¨º¥![]() £ª
£ª
![]() “¿Ã‚“‚µ√£¨
“¿Ã‚“‚µ√£¨![]()
Ω‚µ√£¨![]() £¨
£¨
”÷![]() Œ™’˚ ˝£¨
Œ™’˚ ˝£¨
![]() £¨2£¨3£Æ
£¨2£¨3£Æ
![]() £¨
£¨
![]() ÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û£¨
ÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û£¨
![]() µ±
µ±![]() ±£¨y”–◊Ó–°÷µ
±£¨y”–◊Ó–°÷µ![]() ‘™£Æ
‘™£Æ
![]() …ËA◊„«Úπ∫¬Úm∏ˆ£¨B◊„«Úπ∫¬Ún∏ˆ£¨“¿Ã‚“‚µ√£¨
…ËA◊„«Úπ∫¬Úm∏ˆ£¨B◊„«Úπ∫¬Ún∏ˆ£¨“¿Ã‚“‚µ√£¨
![]() £Æ
£Æ
![]()
Ω‚µ√![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() £Æ
£Æ
![]() £¨34£¨31£Æ
£¨34£¨31£Æ
π ¥∞∏Œ™31£¨34£¨37£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() µƒ¥π÷±∆Ω∑÷œþ
µƒ¥π÷±∆Ω∑÷œþ![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨Ωª
£¨Ωª![]() ”⁄µ„
”⁄µ„![]() £Æ
£Æ
£®1£©»Ù![]() £¨«Û
£¨«Û![]() µƒ∂» ˝£ª
µƒ∂» ˝£ª
£®2£©»Ù![]() £¨
£¨![]() µƒ÷Ð≥§Œ™
µƒ÷Ð≥§Œ™![]() £¨«Û
£¨«Û![]() µƒ≥§£Æ
µƒ≥§£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy=ax2+2x©Å3”Îx÷·Ωª”⁄A°¢B¡Ωµ„£¨«“B£®1£¨0£©
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω∫Õµ„Aµƒ◊¯±Í£ª
£®2£©»ÁÕº1£¨µ„P «÷±œþy=x…œµƒ∂ص„£¨µ±÷±œþy=x∆Ω∑÷°œAPB ±£¨«Ûµ„Pµƒ◊¯±Í£ª
£®3£©»ÁÕº2£¨“—÷™÷±œþy= ![]() x©Å
x©Å ![]() ∑÷±”Îx÷·°¢y÷·Ωª”⁄C°¢F¡Ωµ„£¨µ„Q «÷±œþCFœ¬∑Ωµƒ≈◊ŒÔœþ…œµƒ“ª∏ˆ∂ص„£¨π˝µ„Q◊˜y÷·µƒ∆Ω––œþ£¨Ωª÷±œþCF”⁄µ„D£¨µ„E‘⁄œþ∂ŒCDµƒ—”≥§œþ…œ£¨¡¨Ω”QE£ÆŒ £∫“‘QDŒ™—¸µƒµ»—¸°˜QDEµƒ√ʪ˝ «∑ҥʑ⁄◊Ó¥Û÷µ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆ’‚∏ˆ◊Ó¥Û÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
∑÷±”Îx÷·°¢y÷·Ωª”⁄C°¢F¡Ωµ„£¨µ„Q «÷±œþCFœ¬∑Ωµƒ≈◊ŒÔœþ…œµƒ“ª∏ˆ∂ص„£¨π˝µ„Q◊˜y÷·µƒ∆Ω––œþ£¨Ωª÷±œþCF”⁄µ„D£¨µ„E‘⁄œþ∂ŒCDµƒ—”≥§œþ…œ£¨¡¨Ω”QE£ÆŒ £∫“‘QDŒ™—¸µƒµ»—¸°˜QDEµƒ√ʪ˝ «∑ҥʑ⁄◊Ó¥Û÷µ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆ’‚∏ˆ◊Ó¥Û÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™÷±œþ![]() ”Îx÷·∫Õ y ÷·∑÷±Ωª”ÎA£¨B ¡Ωµ„£¨¡Ì“ª÷±œþæ≠π˝µ„B∫Õµ„C£®6£¨£≠5£©£Æ
”Îx÷·∫Õ y ÷·∑÷±Ωª”ÎA£¨B ¡Ωµ„£¨¡Ì“ª÷±œþæ≠π˝µ„B∫Õµ„C£®6£¨£≠5£©£Æ
£®1£©«Û A£¨B ¡Ωµ„µƒ◊¯±Í£ª
£®2£©÷§√˜£∫°˜ABC «÷±Ω«»˝Ω«–Œ£ª
£®3£©‘⁄ x ÷·…œ’““ªµ„ P£¨ π°˜BCP «“‘ BC Œ™µ◊±þµƒµ»—¸»˝Ω«–Œ£¨«Û≥ˆ P µ„◊¯±Í£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø≈◊ŒÔœþ ![]() µƒ∂•µ„Œ™
µƒ∂•µ„Œ™ ![]() £¨”Î
£¨”Î ![]() ÷·µƒ“ª∏ˆΩªµ„
÷·µƒ“ª∏ˆΩªµ„ ![]() ‘⁄µ„(-3, 0)∫Õ(-2 ,0)÷ƺ‰£¨∆‰≤ø∑÷ÕºœÛ»ÁÕº£¨‘Ú“‘œ¬Ω·¬€:¢Ÿ
‘⁄µ„(-3, 0)∫Õ(-2 ,0)÷ƺ‰£¨∆‰≤ø∑÷ÕºœÛ»ÁÕº£¨‘Ú“‘œ¬Ω·¬€:¢Ÿ ![]() <0 ;¢⁄
<0 ;¢⁄ ![]() <0;¢€
<0;¢€ ![]() =2;¢Ð∑Ω≥Ã
=2;¢Ð∑Ω≥à ![]() ”–¡Ω∏ˆœýµ»µƒ µ ˝∏˘£¨∆‰÷–’˝»∑Ω·¬€µƒ∏ˆ ˝Œ™∏ˆ.
”–¡Ω∏ˆœýµ»µƒ µ ˝∏˘£¨∆‰÷–’˝»∑Ω·¬€µƒ∏ˆ ˝Œ™∏ˆ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
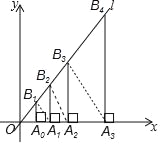
°æƒø°ø»ÁÕº£¨π˝µ„A0£®1£¨0£©◊˜x÷·µƒ¥πœþ£¨Ωª÷±œþl£∫y£Ω2x”⁄B1£¨‘⁄x÷·…œ»°µ„A1£¨ πOA1£ΩOB1£¨π˝µ„A1◊˜x÷·µƒ¥πœþ£¨Ωª÷±œþl”⁄B2£¨‘⁄x÷·…œ»°µ„A2£¨ πOA2£ΩOB2£¨π˝µ„A2◊˜x÷·µƒ¥πœþ£¨Ωª÷±œþl”⁄B3£¨°≠£¨’‚—˘“¿¥Œ◊˜Õº£¨‘Úµ„B8µƒ◊ð◊¯±ÍŒ™£®°°°°£©
A. £®![]() £©7B. 2£®
£©7B. 2£®![]() £©7C. 2£®
£©7C. 2£®![]() £©8D. £®
£©8D. £®![]() £©9
£©9
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø°∞ŒÂ“ª°±∆⁄º‰£¨–°∫ÏµΩƒ≥æ∞«¯µ«…Ω”ŒÕÊ£¨–°∫Ï…œ…Ω ±º‰x£®∑÷÷”£©”Î◊þπ˝µƒ¬∑≥Ãy£®√◊£©÷ƺ‰µƒ∫Ø ˝πÿœµ»ÁÕºÀ˘ 棨‘⁄–°∫Ï≥ˆ∑¢µƒÕ¨ ±¡Ì“ª√˚”ŒøÕ–°ªÐ’˝‘⁄æý¿Î…Ωµ◊60√◊¥¶—ÿœýÕ¨œþ¬∑…œ…Ω£¨»Ù–°∫Ï…œ…Ωπ˝≥Ã÷–”Ζ°ªÐ«°∫√”–¡Ω¥Œœý”ˆ£¨‘Ú–°ªÐ…œ…Ω∆Ωæ˘ÀŸ∂»v£®√◊/∑÷÷”£©µƒ»°÷µ∑∂Œß «_____£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø ˝—ß–À»§ªÓ∂ØøŒ…œ£¨–°√˜Ω´µ»—¸°˜ABCµƒµ◊±þBC”Î÷±œþ1÷ÿ∫œ£¨Œ £∫
£®1£©“—÷™AB£ΩAC£Ω6£¨°œBAC£Ω120°„£¨µ„P‘⁄BC±þÀ˘‘⁄µƒ÷±œþl…œ“∆∂Ø£¨∏˘æð°∞÷±œþÕ‚“ªµ„µΩ÷±œþ…œÀ˘”–µ„µƒ¡¨œþ÷–¥πœþ∂Œ◊Ó∂𱣨–°√˜∑¢œ÷APµƒ◊Ó–°÷µ «°° °°£ª
£®2£©Œ™Ω¯“ª≤Ω‘À”√∏√Ω·¬€£¨–°√˜∑¢œ÷µ±AP◊Ó∂à ±£¨‘⁄Rt°˜ABP÷–£¨°œP£Ω90°„£¨◊˜¡ÀAD∆Ω∑÷°œBAP£¨ΩªBP”⁄µ„D£¨µ„E°¢F∑÷± «AD°¢AP±þ…œµƒ∂ص„£¨¡¨Ω”PE°¢EF£¨–°√˜≥¢ ‘ÃΩÀ˜PE+EFµƒ◊Ó–°÷µ£¨Œ™◊™ªØEF£¨–°√˜‘⁄AB…œΩÿ»°AN£¨ πµ√AN£ΩAF£¨¡¨Ω”NE£¨“◊÷§°˜AEF°’°˜AEN£¨¥”∂¯Ω´PE+EF◊™ªØŒ™PE+EN£¨◊™ªØµΩ£®1£©µƒ«Èøˆ£¨»ÙBP£Ω3![]() £¨AB£Ω6£¨AP£Ω3£¨‘ÚPE+EFµƒ◊Ó–°÷µŒ™°° °°£ª
£¨AB£Ω6£¨AP£Ω3£¨‘ÚPE+EFµƒ◊Ó–°÷µŒ™°° °°£ª
£®3£©«Î”¶”√“‘…œ◊™ªØÀºœÎΩ‚æˆŒ £®3£©£¨‘⁄÷±Ω«°˜ABC÷–£¨°œC£Ω90°„£¨°œB£Ω30°„£¨AC£Ω10£¨µ„D «CD±þ…œµƒ∂ص„£¨¡¨Ω”AD£¨Ω´œþ∂ŒADÀ≥ ±’Ζ˝◊™60°„£¨µ√µΩœþ∂ŒAP£¨¡¨Ω”CP£¨«Ûœþ∂ŒCPµƒ◊Ó–°÷µ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø¡·¡·º“◊º±∏◊∞–Þ“ªÃ◊–¬◊°∑ø£¨»Ùº◊°¢““¡Ω∏ˆ◊∞ Œπ´Àæ∫œ◊˜£¨–Ë6÷ÐÕÍ≥…£¨π≤–Ë◊∞–Þ∑—Œ™5.2ÕÚ‘™£ª»Ùº◊π´À浕∂¿◊ˆ4÷Ð∫Û£¨ £œ¬µƒ”…““π´Àæ¿¥◊ˆ£¨ªπ–Ë9÷Ð≤≈ƒÐÕÍ≥…£¨π≤–Ë◊∞–Þ∑—4.8ÕÚ‘™.¡·¡·µƒ∞÷∞÷¬Ë¬Ë…áø∫Ûæˆ∂®÷ª—°“ª∏ˆπ´À浕∂¿ÕÍ≥….
£®1£©»Áπ˚¥”Ω⁄‘º ±º‰µƒΩ«∂»øº¬«”¶—°ƒƒº“π´Àæ£ø
£®2£©»Áπ˚¥”Ω⁄‘ºø™÷ßµƒΩ«∂»øº¬«ƒÿ£ø«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com