
如图,在⊙O中,半径OC与弦AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点.若OE=4,OF=6,求⊙O的半径和CD的长.

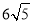
【解析】
试题分析:由OE⊥AB得到∠OEF=90°,再根据圆周角定理由OC为小圆的直径得到∠OFC=90°,则可证明Rt△OEF∽Rt△OFC,然后利用相似比可计算出CD=9;接着在Rt△OCF中,根据勾股定理可计算出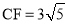 ,由于OF⊥CD,根据垂径定理得CF=DF,所以
,由于OF⊥CD,根据垂径定理得CF=DF,所以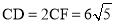 .
.
试题解析:∵OE⊥AB,
∴∠OEF=90°,
∵OC为小圆的直径,
∴∠OFC=90°,
而∠EOF=∠FOC,
∴Rt△OEF∽Rt△OFC,
∴OE:OF=OF:OC,即4:6=6:CD,
∴CD=9;
在Rt△OCF中,OF=6,OC=9,
∴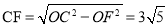 ,
,
∵OF⊥CD,
∴CF=DF,
∴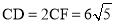 .
.
考点:垂径定理;勾股定理;圆周角定理;相似三角形的判定与性质.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源:2014年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:解答题
已知关于x的方程 .
.
(1)当该方程的一个根为1时,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(山东滨州卷)数学(解析版) 题型:选择题
如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )

A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.两直线平行,同位角相等 D.两直线平行,内错角相等
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(山东济宁卷)数学(解析版) 题型:选择题
“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程 的两根,且a < b, 则a、b、m、n 的大小关系是( )
的两根,且a < b, 则a、b、m、n 的大小关系是( )
A.m < a < b< n B.a < m < n < b C.a < m < b< n D.m < a < n < b
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(安徽卷)数学(解析版) 题型:填空题
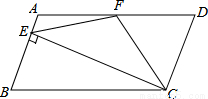
如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=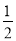 ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(安徽卷)数学(解析版) 题型:选择题
已知x2—2x—3=0,则2x2—4x的值为( )
A.—6 B.6 C.—2或6, D.—2或30
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川资阳卷)数学(解析版) 题型:解答题
某商家计划从厂家采购空调和冰箱两种产品共20台,空调的采购单价y1(元/台)与采购数量x1(台)满足y1=﹣20x1+1500(0<x1≤20,x1为整数);冰箱的采购单价y2(元/台)与采购数量x2(台)满足y2=﹣10x2+1300(0<x2≤20,x2为整数).
(1)经商家与厂家协商,采购空调的数量不少于冰箱数量的 ,且空调采购单价不低于1200元,问该商家共有几种进货方案?
,且空调采购单价不低于1200元,问该商家共有几种进货方案?
(2)该商家分别以1760元/台和1700元/台的销售单价售出空调和冰箱,且全部售完.在(1)的条件下,问采购空调多少台时总利润最大?并求最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com