
����Ŀ����ͼ1���Ǽס�������Բ����ˮ�۵������ʾ��ͼ���Ҳ�����һ�����������������У�Բ����������µ�����ȫ�����Ҳ۵����ϣ�.�ֽ��ײ۵�ˮ����ע���Ҳۣ��ס�������ˮ����ˮ�����y�����ף���עˮʱ��x�����ӣ�֮��Ĺ�ϵ��ͼ2��ʾ������ͼ���ṩ����Ϣ������������⣺
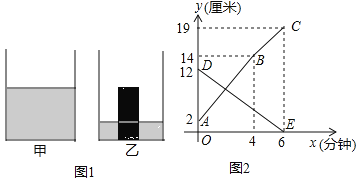
��1��ͼ2������ABC��ʾ ����ˮ�������עˮʱ���ϵ���߶�DE��ʾ ����ˮ�������עˮʱ��֮��Ĺ�ϵ����������ѡ��ס����ҡ�������B���������ʾ��ʵ�������� .
��2��עˮ�ʱ��ʱ���ס���.����ˮ����ˮ�������ͬ��
��3�����Ҳ۵����Ϊ36ƽ�����ף��ںƣ������Ҳ�����������Ϊ ��������.
���𰸡���1���ң��ף��Ҳ�������ĸ߶�Ϊ14cm����2����2����ʱ����ˮ��ˮ��һ���ߣ���3��84.
��������
��1��������Ŀ�мײ����Ҳ�עˮ���Եõ�����ABC���Ҳ���ˮ�������עˮʱ��֮��Ĺ�ϵ����B��ʾ��ʵ���������Ҳ���Һ��ǡ����Բ�������鶥����ƽ��
��2���ֱ��������ˮ����y��x�ĺ�����ϵʽ����y��ȼ��ɵõ�ˮλ��ȵ�ʱ�䣻
��3����ˮ�۵������ȥˮ����ˮ��������ɵõ�����������
�⣺��1������ͼ���֪������ABC��ʾ�Ҳ���ˮ�������עˮʱ���ϵ���߶�DE��ʾ�ײ���ˮ�������עˮʱ��֮��Ĺ�ϵ����B���������ʾ��ʵ�������ǣ��Ҳ�������ĸ߶�Ϊ14cm��
�ʴ�Ϊ���ң��ף��Ҳ�������ĸ߶�Ϊ14cm��
��2�����߶�AB��DE�Ľ���ʽ�ֱ�Ϊ��y1=k1x+b1��y2=k2x+b2��
��AB�����㣨0��2���ͣ�4��14����DE������0��12���ͣ�6��0��
��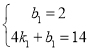 ��
��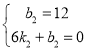
��ã�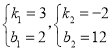 ��
��
�����ʽΪy=3x+2��y=-2x+12��
��3x+2=-2x+12��
���x=2��
�൱2����ʱ����ˮ��ˮ��һ���ߣ�
��3����ͼ��֪����ˮ����û��û������ʱ4����ˮ��������12cm����1��������3cm��
��ˮ��û������ʱ��2����������5cm����1��������2.5cm��
������ĵ����Ϊacm2������ˮ���в������������ֱ�Ϊ��2.5��36cm3��
���������������3����36-a��cm3��
��1��3����36-a��=1��2.5��36��
���a=6��
������������6��14=84��cm3����
�ʴ�Ϊ��84.


 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ѱ�����ȫ��ͬ���˿ˣ���һ������ֱ�д������1��2��3��4���ڶ�������ֱ�д������1��2��3���ֱ��Ϻ�С��ӵ�һ���������ȡһ�ţ��ѿ�Ƭ�ϵ�������Ϊ��������С�ݴӵڶ����������ȡһ�ţ��ѿ�Ƭ�ϵ�������Ϊ������Ȼ���������������IJ
��1�����û���״ͼ���б��ķ���������������Ϊ0�ĸ��ʣ�
��2��С����С������Ϸ�������ǣ����������IJ�Ϊ�Ǹ�������С��ʤ������С��ʤ������Ϊ����Ϸ����ƽ�������ƽ����˵�����ɣ��������ƽ����������Ϸ����ʹ��Ϸ��ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
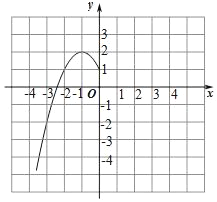
����Ŀ��ij�ࡰ��ѧ��ȤС�顱�Ժ���y����x2+2|x|+1��ͼ������ʽ�����̽����̽���������£��벹��������
��1���Ա���x��ȡֵ��Χ��ȫ��ʵ����x��y�ļ����Ӧֵ�б����£�
x | �� | ��3 | �� | ��2 | ��1 | 0 | 1 | 2 |
| 3 | �� |
y | �� | ��2 | �� | m | 2 | 1 | 2 | 1 | �� | ��2 | �� |
����m���� ����
��2�������ϱ����ݣ�����ͼ��ʾ��ƽ��ֱ������ϵ����㣬�����˺���ͼ���һ���֣��뻭���ú���ͼ�����һ���֣�
��3���۲캯��ͼ��д���������������ʣ�
��4����һ��̽������ͼ���֣�
�����̩�x2+2|x|+1��0���� ����ʵ������
������x�ķ��̩�x2+2|x|+1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
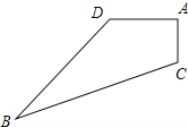
����Ŀ����֪ijʵ����ѧ��һ���ı��εĿյ�ABCD����ͼ��ʾ��ѧУ�ƻ��ڿյ�����ֲ��ƺ����������A=90�㣬AC=3m��BD=12m��CB=13m��DA=4m����ÿƽ���ײ�ƺ��Ҫ300Ԫ����ѧУ��ҪͶ������ʽ����ƺ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� Ϊ���¹���Ʒ�֣�ij���ƻ��¹���A��B����Ʒ�ֵĹ�������ֲ���������ƻ����������ֹ����繲45�ã�����A����ĵ���Ϊ7Ԫ/�ã�����B�����������y��Ԫ���빺������x���ã�֮�������ͼ��ʾ�ĺ�����ϵ��
��1����y��x�ĺ�����ϵʽ��
��2�����ڹ���ƻ��У�B���������������35�ã���������A���������������ƹ�����ʹ�ܷ�����ͣ��������ͷ��ã�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾������ij�ֲ�Ʒÿ���ɱ�Ϊ40Ԫ�����г�����������������Ϣ��
�ٸò�Ʒ90��������������m������ʱ�䣨��x�죩����һ�κ�����ϵ�������������±���
ʱ�䣨��x�죩 | 1 | 3 | 6 | 10 | �� |
����������m���� | 198 | 194 | 188 | 180 | �� |
�ڸò�Ʒ90����ÿ������ۼ۸���ʱ�䣨��x�죩�Ĺ�ϵ���±���
ʱ�䣨��x�죩 | 1��x��50 | 50��x��90 |
���ۼ۸�Ԫ/���� | x+60 | 100 |
��1����m����x��һ�κ�������ʽ��
��2�������۸ò�Ʒÿ������ΪyԪ����д��y����x�ĺ�������ʽ���������90���ڸò�Ʒ������������������������Ƕ��٣�����ʾ��ÿ����������=������������ÿ�����ۼ۸�-ÿ���ɱ�����
��3���ڸò�Ʒ���۵Ĺ����У����ж���������������5400Ԫ����ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����н��ۣ�
��b��0����4a+2b+c��0����a��b+c��0������a+c��2��b2��������ȷ�Ľ�����
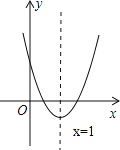
A���٢� B���٢� C���٢ۢ� D���٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ŵȿ���ֽ�������ص���һ���ص��IJ���Ϊ�ı���ABCD�������A��C֮��ľ���Ϊ6cm����B��D֮��ľ���Ϊ8cm�����߶�AB�ij�Ϊ��������
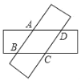
A.5 cmB.4.8 cmC.4.6 cmD.4 cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1��y1=-![]() x+m��y�ύ�ڵ�A(0��6)��ֱ��l2��y2=kx+1�ֱ���x�ύ�ڵ�B(-2��0)����y�ύ�ڵ�C������ֱ��l1��l2�ཻ�ڵ�D������AB��
x+m��y�ύ�ڵ�A(0��6)��ֱ��l2��y2=kx+1�ֱ���x�ύ�ڵ�B(-2��0)����y�ύ�ڵ�C������ֱ��l1��l2�ཻ�ڵ�D������AB��
(1)����ֱ��l1��l2����D�����ꣻ
(2)���ABD�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com