
°æƒø°øƒ≥∞ý°∞ ˝—ß–À»§–°◊È°±∂‘∫Ø ˝y£Ω©Åx2+2|x|+1µƒÕºœÛ∫Õ–‘÷ Ω¯––¡ÀÃΩæø£¨ÃΩæøπ˝≥ûÁœ¬£¨«Î≤π≥‰ÕÍ’˚£Æ
£®1£©◊‘±‰¡øxµƒ»°÷µ∑∂Œß «»´Ã µ ˝£¨x”Îyµƒº∏◊È∂‘”¶÷µ¡–±Ì»Áœ¬£∫
x | °≠ | ©Å3 | ©Å | ©Å2 | ©Å1 | 0 | 1 | 2 |
| 3 | °≠ |
y | °≠ | ©Å2 | ©Å | m | 2 | 1 | 2 | 1 | ©Å | ©Å2 | °≠ |
∆‰÷–£¨m£Ω°° °°£Æ
£®2£©∏˘æð…œ±Ì ˝æ𣨑⁄»ÁÕºÀ˘ 浃∆Ω√Ê÷±Ω«◊¯±Íœµ÷–√˵„£¨ª≠≥ˆ¡À∫Ø ˝ÕºœÛµƒ“ª≤ø∑÷£¨«Îª≠≥ˆ∏√∫Ø ˝ÕºœÛµƒ¡Ì“ª≤ø∑÷£Æ
£®3£©π€≤Ï∫Ø ˝ÕºœÛ£¨–¥≥ˆ¡ΩÃı∫Ø ˝µƒ–‘÷ £Æ
£®4£©Ω¯“ª≤ΩÃΩæø∫Ø ˝ÕºœÛ∑¢œ÷£∫
¢Ÿ∑Ω≥éÅx2+2|x|+1£Ω0”–°° °°∏ˆ µ ˝∏˘£ª
¢⁄πÿ”⁄xµƒ∑Ω≥éÅx2+2|x|+1£Ω
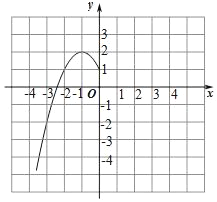
°æ¥∞∏°ø£®1£©1£ª£®2£©œÍº˚Ω‚Œˆ£ª£®3£©¢Ÿ∫Ø ˝µƒ◊Ó¥Û÷µ «2£¨√ª”–◊Ó–°÷µ£ª¢⁄µ±x£æ1 ±£¨yÀÊxµƒ‘ˆ¥Û∂¯ºı–°£ª£®4£©¢Ÿ2£ª¢⁄1£ºa£º2£Æ
°æΩ‚Œˆ°ø
£®1£©∏˘æð∂‘≥∆ø…µ√m=1£ª
£®2£©ª≠≥ˆÕº–Œ£ª
£®3£©¢Ÿ–¥∫Ø ˝µƒ◊Ó¥Û÷µ∫Õ◊Ó–°÷µŒ £ª
¢⁄»∑∂®“ª∏ˆ∑∂Œß–¥‘ˆºı–‘Œ £ª
£®4£©¢Ÿµ±y=0 ±£¨”Îx÷·µƒΩªµ„”–¡Ω∏ˆ£¨‘Ú”–2∏ˆ µ ˝∏˘£ª
¢⁄µ±y=a ±£¨”–4∏ˆ µ∏˘£¨æÕ «”–4∏ˆΩªµ„£¨»∑∂®∆‰aµƒ÷µº¥ø…£Æ
Ω‚£∫£®1£©”…±Ì∏Òø…÷™£∫ÕºœÛµƒ∂‘≥∆÷· «y÷·£¨
°ým£Ω1£¨
π ¥∞∏Œ™£∫1£ª
£®2£©»ÁÕºÀ˘ 棪
£®3£©–‘÷ £∫¢Ÿ∫Ø ˝µƒ◊Ó¥Û÷µ «2£¨√ª”–◊Ó–°÷µ£ª
¢⁄µ±x£æ1 ±£¨yÀÊxµƒ‘ˆ¥Û∂¯ºı–°£ª
£®4£©¢Ÿ”…ÕºœÛµ√£∫≈◊ŒÔœþ”Îx÷·”–¡Ω∏ˆΩªµ„
°ý∑Ω≥éÅx2+2|x|+1£Ω0”–2∏ˆ µ ˝∏˘£ª
π ¥∞∏Œ™£∫2£ª
¢⁄”…ÕºœÛø…÷™£∫©Åx2+2|x|+1£Ωa”–4∏ˆ µ ˝∏˘ ±£¨
º¥y£Ωa ±£¨”ÎÕºœÛ”–4∏ˆΩªµ„£¨
À˘“‘aµƒ»°÷µ∑∂Œß «£∫1£ºa£º2£Æ
π ¥∞∏Œ™£∫1£ºa£º2£Æ


 ƒÐ¡¶∆¿º€œµ¡–¥∞∏
ƒÐ¡¶∆¿º€œµ¡–¥∞∏ Ã∆”°ŒƒªØøŒ ±≤‚∆¿œµ¡–¥∞∏
Ã∆”°ŒƒªØøŒ ±≤‚∆¿œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥…Ã∆∑µƒΩ¯º€Œ™√øº˛50‘™£Æµ± €º€Œ™√øº˛70‘™ ±£¨√ø–«∆⁄ø…¬Ù≥ˆ300º˛£¨œ÷–ËΩµº€¥¶¿Ì£¨«“æ≠ –≥°µ˜≤È£∫√øΩµº€1‘™£¨√ø–«∆⁄ø…∂ý¬Ù≥ˆ20º˛£Æ‘⁄»∑±£”Ø¿˚µƒ«∞÷œ¬£¨Ω‚¥œ¬¡–Œ £∫
£®1£©»Ù…Ë√øº˛Ωµº€x‘™°¢√ø–«∆⁄ €≥ˆ…Ã∆∑µƒ¿˚»ÛŒ™y‘™£¨«Î–¥≥ˆy”Îxµƒ∫Ø ˝πÿœµ Ω£¨≤¢«Û≥ˆ◊‘±‰¡øxµƒ»°÷µ∑∂Œß£ª
£®2£©µ±Ωµº€∂ý…Ÿ‘™ ±£¨√ø–«∆⁄µƒ¿˚»Û◊Ó¥Û£ø◊Ó¥Û¿˚»Û «∂ý…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄µØª…œÞ∂»ƒ⁄£¨µØª…π“…œŒÔÃÂ∫۵ت…µƒ≥§∂»”ÎÀ˘π“ŒÔõƒ÷ ¡ø÷ƺ‰µƒπÿœµ»Áœ¬±Ì£∫
À˘π“ŒÔõƒ÷ ¡ø/«ßøÀ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
µØª…µƒ≥§∂»/ | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
£®1£©µØª…≤ªπ“ŒÔà±µƒ≥§∂» «∂ý…Ÿ£ø
£®2£©»Áπ˚”√![]() ±Ì æµØ–‘œÞ∂»ƒ⁄ŒÔõƒ÷ ¡ø£¨”√
±Ì æµØ–‘œÞ∂»ƒ⁄ŒÔõƒ÷ ¡ø£¨”√![]() ±Ì æµØª…µƒ≥§∂»£¨–¥≥ˆ
±Ì æµØª…µƒ≥§∂»£¨–¥≥ˆ![]() ”Î
”Î![]() µƒπÿœµ Ω£Æ
µƒπÿœµ Ω£Æ
£®3£©»Áπ˚¥À ±µØª…◊Ó¥Ûπ“÷ÿ¡øŒ™25«ßøÀ£¨ƒ„ƒÐ‘§≤‚µ±π“÷ÿŒ™14«ßøÀ ±£¨µØª…µƒ≥§∂» «∂ý…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœþy1=©Åx2+4x∫Õ÷±œþy2=2x£ÆŒ“√«πÊ∂®£∫µ±x»°»Œ“‚“ª∏ˆ÷µ ±£¨x∂‘”¶µƒ∫Ø ˝÷µ∑÷±Œ™y1∫Õy2£¨»Ùy1°Ÿy2£¨»°y1∫Õy2÷–Ωœ–°÷µŒ™M£ª»Ùy1=y2£¨º«M=y1=y2£Æ¢Ÿµ±x£æ2 ±£¨M=y2£ª¢⁄µ±x£º0 ±£¨MÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û£ª¢€ πµ√M¥Û”⁄4µƒxµƒ÷µ≤ª¥Ê‘⁄£ª¢Ð»ÙM=2£¨‘Úx=1£Æ…œ ˆΩ·¬€’˝»∑µƒ «_____£®ÃÓ–¥À˘”–’˝»∑Ω·¬€µƒ–Ú∫≈£©£Æ
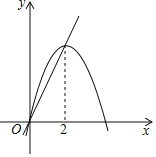
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() µƒ∂‘±þ∑÷±º«Œ™
µƒ∂‘±þ∑÷±º«Œ™![]() £¨
£¨![]() £¨
£¨![]() £¨”…œ¬¡–Ãıº˛≤ªƒÐ≈–∂®
£¨”…œ¬¡–Ãıº˛≤ªƒÐ≈–∂®![]() Œ™÷±Ω«»˝Ω«–Œµƒ «£® £©
Œ™÷±Ω«»˝Ω«–Œµƒ «£® £©
A.![]() B.
B.![]()
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
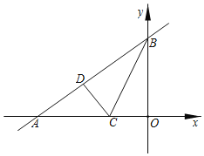
°æƒø°ø»ÁÕº£¨‘⁄“ª∏ˆø…“‘◊‘”…◊™∂صƒ◊™≈Ã÷–£¨÷∏’ÎŒª÷√πÃ∂®£¨»˝∏ˆ…»–Œµƒ√ʪ˝∂ºœýµ»£¨«“∑÷±±Í”– ˝◊÷1£¨2£¨3£Æ

£®1£©–°√˜◊™∂Ø◊™≈Óª¥Œ£¨µ±◊™≈ÃÕ£÷π◊™∂Ø ±£¨÷∏’ÎÀ˘÷∏…»–Œ÷–µƒ ˝◊÷ «∆Ê ˝µƒ∏≈¬ Œ™________£ª
£®2£©–°√˜œ»◊™∂Ø◊™≈Óª¥Œ£¨µ±◊™≈ÃÕ£÷π◊™∂Ø ±£¨º«¬ºœ¬÷∏’ÎÀ˘÷∏…»–Œ÷–µƒ ˝◊÷£ªΩ”◊≈‘Ÿ◊™∂Ø◊™≈Óª¥Œ£¨µ±◊™≈ÃÕ£÷π◊™∂Ø ±£¨‘Ÿ¥Œº«¬ºœ¬÷∏’ÎÀ˘÷∏…»–Œ÷–µƒ ˝◊÷£¨«Û’‚¡Ω∏ˆ ˝◊÷÷Æ∫Õ «3µƒ±∂ ˝µƒ∏≈¬ (”√ª≠ ˜◊¥ÕºªÚ¡–±Ìµ»∑Ω∑®«ÛΩ‚)
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫÷±œþ![]() ”Î
”Î![]() ÷·°¢
÷·°¢![]() ÷·∑÷±œýΩª”⁄µ„
÷·∑÷±œýΩª”⁄µ„![]() ∫Õµ„
∫Õµ„![]() £¨µ„
£¨µ„![]() ‘⁄œþ∂Œ
‘⁄œþ∂Œ![]() …œ£ÆΩ´
…œ£ÆΩ´![]() —ÿ
—ÿ![]() ’€µ˛∫Û£¨µ„
’€µ˛∫Û£¨µ„![]() «°∫√¬‰‘⁄
«°∫√¬‰‘⁄![]() ±þ…œµ„
±þ…œµ„![]() ¥¶£Æ
¥¶£Æ
£®1£©÷±Ω”–¥≥ˆµ„![]() °¢µ„
°¢µ„![]() µƒ◊¯±Í£∫
µƒ◊¯±Í£∫
£®2£©«Û![]() µƒ≥§£ª
µƒ≥§£ª
£®3£©µ„![]() Œ™∆Ω√ʃ⁄“ª∂ص„£¨«“¬˙◊„“‘
Œ™∆Ω√ʃ⁄“ª∂ص„£¨«“¬˙◊„“‘![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() Œ™∂•µ„µƒÀƒ±þ–ŒŒ™∆Ω––Àƒ±þ–Œ£¨«Î÷±Ω”ªÿ¥£∫
Œ™∂•µ„µƒÀƒ±þ–ŒŒ™∆Ω––Àƒ±þ–Œ£¨«Î÷±Ω”ªÿ¥£∫
¢Ÿ∑˚∫œ“™«Ûµƒ![]() µ„”–º∏∏ˆ£ø
µ„”–º∏∏ˆ£ø
¢⁄–¥≥ˆ“ª∏ˆ∑˚∫œ“™«Ûµƒ![]() µ„◊¯±Í£Æ
µ„◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨ «º◊°¢““¡Ω∏ˆ‘≤÷˘–ŒÀÆ≤€µƒ÷·Ωÿ√Ê æ“‚Õº£¨““≤€÷–”–“ªÀƒ÷˘–ŒÃ˙øÈ¡¢∑≈∆‰÷–£®‘≤÷˘–ŒÃ˙øȵƒœ¬µ◊√ÊÕÍ»´¬‰‘⁄““≤€µ◊√Ê…œ£©.œ÷Ω´º◊≤€µƒÀÆ‘»ÀŸ◊¢»Î““≤€£¨º◊°¢““¡Ω∏ˆÀÆ≤€÷–ÀƵƒ…Ó∂»y£®¿Â√◊£©”Î◊¢ÀÆ ±º‰x£®∑÷÷”£©÷ƺ‰µƒπÿœµ»ÁÕº2À˘ 棨∏˘æðÕºœÛÃ·π©µƒ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
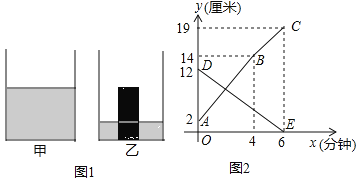
£®1£©Õº2÷–’€œþABC±Ì æ ≤€÷–ÀƵƒ…Ó∂»”Î◊¢ÀÆ ±º‰πÿœµ£¨œþ∂ŒDE±Ì æ ≤€÷–ÀƵƒ…Ó∂»”Î◊¢ÀÆ ±º‰÷ƺ‰µƒπÿœµ£®“‘…œ¡Ωø’—°ÃÓ°∞º◊°±ªÚ°∞““°±£©£¨µ„Bµƒ◊ð◊¯±Í±Ì 浃 µº “‚“ « .
£®2£©◊¢ÀÆ∂ý≥§ ±º‰ ±£¨º◊°¢““.¡Ω∏ˆÀÆ≤€÷–ÀƵƒ…Ó∂»œýÕ¨£ø
£®3£©»Ù““≤€µ◊√ʪ˝Œ™36∆Ω∑Ω¿Â√◊£®±⁄∫Ò≤ªº∆£©£¨‘Ú““≤€÷–Ã˙øȵƒÃª˝Œ™ ¡¢∑Ω¿Â√◊.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥π§≥ߺ∆ªÆ…˙≤˙º◊°¢““¡Ω÷÷≤˙∆∑π≤2500∂÷£¨√ø…˙≤˙1∂÷º◊≤˙∆∑ø…ªÒµ√¿˚»Û0.3ÕÚ‘™£¨√ø…˙≤˙1∂÷““≤˙∆∑ø…ªÒµ√¿˚»Û0.4ÕÚ‘™£Æ…Ë∏√π§≥ß…˙≤˙¡Àº◊≤˙∆∑x£®∂÷£©£¨…˙≤˙º◊°¢““¡Ω÷÷≤˙∆∑ªÒµ√µƒ◊п˚»ÛŒ™y£®ÕÚ‘™£©£Æ
£®1£©«Ûy”Îx÷ƺ‰µƒ∫Ø ˝±Ì¥Ô Ω£ª
£®2£©»Ù√ø…˙≤˙1∂÷º◊≤˙∆∑–Ë“™A‘≠¡œ0.25∂÷£¨√ø…˙≤˙1∂÷““≤˙∆∑–Ë“™A‘≠¡œ0.5∂÷£Æ Ð –≥°”∞œÏ£¨∏√≥߃Ъҵ√µƒA‘≠¡œ÷¡∂ýŒ™1000∂÷£¨∆‰À¸‘≠¡œ≥‰◊„£Æ«Û≥ˆ∏√π§≥ß…˙≤˙º◊°¢““¡Ω÷÷≤˙∆∑∏˜Œ™∂ý…Ÿ∂÷ ±£¨ƒÐªÒµ√◊Ó¥Û¿˚»Û£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com