
【题目】已知:直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() ,点
,点![]() 在线段
在线段![]() 上.将
上.将![]() 沿
沿![]() 折叠后,点
折叠后,点![]() 恰好落在
恰好落在![]() 边上点
边上点![]() 处.
处.
(1)直接写出点![]() 、点
、点![]() 的坐标:
的坐标:
(2)求![]() 的长;
的长;
(3)点![]() 为平面内一动点,且满足以
为平面内一动点,且满足以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,请直接回答:
为顶点的四边形为平行四边形,请直接回答:
①符合要求的![]() 点有几个?
点有几个?
②写出一个符合要求的![]() 点坐标.
点坐标.
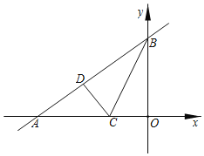
【答案】(1)A(-8,0)、B(0,6);(2)5;(3)①3个;②(-5,6)或(-11,-6)或(5,6).
【解析】
(1)利用待定系数法解决问题即可.
(2)由翻折不变性可知,OC=CD,OB=BD=6,∠ODB=∠BOC=90°,推出AD=AB-BD=4,设CD=OC=x,在Rt△ADC中,根据AD2+CD2=AC2,构建方程即可解决问题.
(3)①根据平行四边形的定义画出图形即可判断.
②利用平行四边形的性质求解即可解决问题.
解:(1)对于直线![]() ,令x=0,得到y=6,
,令x=0,得到y=6,
∴B(0,6),
令y=0,得到x=![]() ,
,
∴A(![]() ,0);
,0);
(2)∵A(![]() ,0),B(0,6),
,0),B(0,6),
∴OA=8,OB=6,
∵∠AOB=90°,
∴![]() ,
,
由翻折不变性可知,OC=CD,OB=BD=6,∠ODB=∠BOC=90°,
∴AD=AB-BD=4,设CD=OC=x,
在Rt△ADC中,∵∠ADC=90°,
∴AD2+CD2=AC2,
∴42+x2=(8-x)2,
解得:x=3,
∴OC=3,AC=OA![]() OC=8
OC=8![]() 3=5.
3=5.
(3)①符合条件的点P有3个,如图所示:
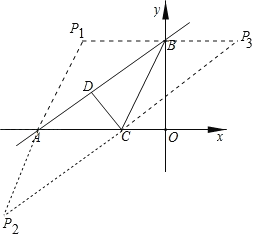
②∵A(-8,0),C(-3,0),B(0,6),
当AB为对角线时,![]() ,
,
由平行四边形的性质,得![]() ,
,
∴P1(-5,6);
当AB为边时,![]() ,点P在第三象限时,有
,点P在第三象限时,有
点B向下平移6个单位,向左平移3个单位得到点C,
∴点A向下平移6个单位,向左平移3个单位得到点P2,
∴P2(-11,-6);
点P在第二象限时,有
![]() ,
,
∴P3(5,6);
∴点P的坐标为:(-5,6)或(-11,-6)或(5,6).


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)2x(2x+5)=(x﹣1)(2x+5) (2)x2+2x﹣5=0.
(3)x2﹣4x﹣1=0 (用公式法) (4)2x2+1=3x(用配方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=﹣x2+2|x|+1的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣2 | ﹣ | m | 2 | 1 | 2 | 1 | ﹣ | ﹣2 | … |
其中,m= .
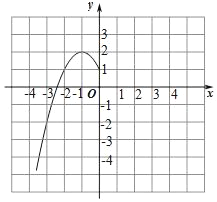
(2)根据上表数据,在如图所示的平面直角坐标系中描点,画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①方程﹣x2+2|x|+1=0有 个实数根;
②关于x的方程﹣x2+2|x|+1=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() ,∠DAB=∠DCB,对角线
,∠DAB=∠DCB,对角线![]() ,
,![]() 交于点
交于点![]() .分别添加下列条件之一:①
.分别添加下列条件之一:①![]() ;②
;②![]() ;③
;③![]() ;④∠ABC=∠ADC,能使四边形
;④∠ABC=∠ADC,能使四边形![]() 成为平行四边形,则正确的选项有_____.(填写序号)
成为平行四边形,则正确的选项有_____.(填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
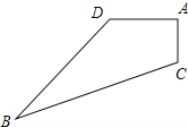
【题目】已知某实验中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草坪,经测量∠A=90°,AC=3m,BD=12m,CB=13m,DA=4m,若每平方米草坪需要300元,间学校需要投入多少资金买草坪?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①b<0;②4a+2b+c<0;③a﹣b+c>0;④(a+c)2<b2.其中正确的结论是
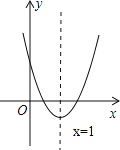
A.①② B.①③ C.①③④ D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com