【题目】已知四边形
，∠DAB=∠DCB，对角线
，
交于点
．分别添加下列条件之一：①
；②
；③
；④∠ABC=∠ADC，能使四边形成为平行四边形，则正确的选项有_____．（填写序号）
【答案】①④
【解析】
根据平行四边形的判定定理：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形．（3）一组对边平行且相等的四边形是平行四边形．（4）两组对角分别相等的四边形是平行四边形．（5）对角线互相平分的四边形是平行四边形进行分析即可．
解：①由AB∥CD，∠DAB=∠DCB可证明∠ABC=∠ADC，然后可根据两组对角分别相等的四边形是平行四边形判定四边形ABCD是平行四边形，故此选项正确；
②根据AB=CD，∠DAB=∠DCB不能判定四边形ABCD是平行四边形，故此选项不正确；
③∠DAB=∠DCB且OA=OC不能判定四边形ABCD是平行四边形，故此选项不正确；
④由∠DAB=∠DCB，∠ABC=∠ADC可根据两组对角分别相等的四边形是平行四边形判定四边形ABCD是平行四边形，故此选项正确．
∴正确的选项有①④；
故答案为：①④．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】阅读下列材料，完成任务：
自相似图形
定义：若某个图形可分割为若干个都与它相似的图形，则称这个图形是自相似图形．例如：正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接EG，HF交于点O，易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形，且与原正方形相似，故正方形是自相似图形．
任务：
（1）图1中正方形ABCD分割成的四个小正方形中，每个正方形与原正方形的相似比为 ；
（2）如图2，已知△ABC中，∠ACB=90°，AC=4，BC=3，小明发现△ABC也是“自相似图形”，他的思路是：过点C作CD⊥AB于点D，则CD将△ABC分割成2个与它自己相似的小直角三角形．已知△ACD∽△ABC，则△ACD与△ABC的相似比为 ；
（3）现有一个矩形ABCD是自相似图形，其中长AD=a，宽AB=b（a＞b）．
请从下列A、B两题中任选一条作答：我选择 题．
A：①如图3﹣1，若将矩形ABCD纵向分割成两个全等矩形，且与原矩形都相似，则a= （用含b的式子表示）；
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形，且与原矩形都相似，则a= （用含n，b的式子表示）；
B：①如图4﹣1，若将矩形ABCD先纵向分割出2个全等矩形，再将剩余的部分横向分割成3个全等矩形，且分割得到的矩形与原矩形都相似，则a= （用含b的式子表示）；
②如图4﹣2，若将矩形ABCD先纵向分割出m个全等矩形，再将剩余的部分横向分割成n个全等矩形，且分割得到的矩形与原矩形都相似，则a= （用含m，n，b的式子表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
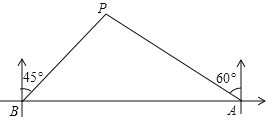
【题目】如图，在一笔直的海岸线l上有A、B两个码头，A在B的正东方向，一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处，此时从B码头测得小船在它的北偏东45°的方向．求此时小船到B码头的距离（即BP的长）和A、B两个码头间的距离（结果都保留根号）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：直线
与
轴、
轴分别相交于点
和点
，点
在线段
上．将
沿
折叠后，点
恰好落在
边上点
处．
（1）直接写出点、点的坐标：
（2）求
的长；
（3）点
为平面内一动点，且满足以、、、为顶点的四边形为平行四边形，请直接回答：
①符合要求的点有几个？
②写出一个符合要求的点坐标．
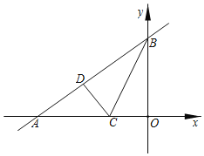
查看答案和解析>>
科目：初中数学 来源： 题型：
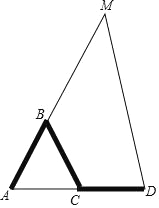
【题目】如图，AB﹣BC﹣CD是一根三节棍，其中线段AB、BC、CD首尾顺次相连，且AB＝BC＝CD，将这个三节棍摆放在△AMD中，使它的两个端点与△AMD两个顶点重合，三节棍的首尾两节在△AMD的边上，则AB﹣BC﹣CD就是△AMD的配套三节棍．
（1）若∠A＝60°，AD＝60，求△AMD的配套三节棍的总长；
（2）若AM＝AD，△AMD的配套三节棍AB﹣BC﹣CD中一边BC平行于MD，利用直尺圆规画出图形，并求出∠A的度数．（保留作图痕迹）
查看答案和解析>>
科目：初中数学 来源： 题型：
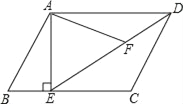
【题目】如图，平行四边形ABCD，AE⊥BC交点E，连接DE，F为DE上一点，且∠AFE＝∠B＝60°．
（1）求证：△ADF∽△DEC；
（2）若AE＝3，AD＝4，求EF的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
