
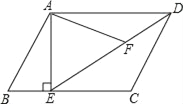
【题目】如图,平行四边形ABCD,AE⊥BC交点E,连接DE,F为DE上一点,且∠AFE=∠B=60°.
(1)求证:△ADF∽△DEC;
(2)若AE=3,AD=4,求EF的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由平行四边形的性质结合等角的补角相等,可得出∠AFD=∠C=120°、AD∥BC,利用平行线的性质可得出∠ADF=∠DEC,进而即可证出△ADF∽△DEC;
(2)由AE及∠B的值可求出BE、CE的长度,在Rt△ADE中,利用勾股定理可求出DE的长度,由△ADF∽△DEC利用相似三角形的性质即可求出DF的长度,再将其代入EF=DE-DF中即可求出EF的长.
(1)证明:∵四边形ABCD为平行四边形,∠AFE=∠B=60°,
∴∠AFD=∠C=120°,AD∥BC,
∴∠ADF=∠DEC,
∴△ADF∽△DEC.
(2)解:∵AE=3,∠B=60°,
∴BE=![]() ,CE=4﹣
,CE=4﹣![]() .
.
在Rt△ADE中,AE=3,AD=4,
∴DE=![]() =5.
=5.
∵△ADF∽△DEC,
∴![]() ,即
,即![]() ,
,
∴DF=![]() ,
,
∴EF=DE﹣DF=![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知点![]() 、点
、点![]() ,动点
,动点![]() 从点
从点![]() 开始在线段
开始在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动,同时动点
移动,同时动点![]() 从点
从点![]() 开始在线段
开始在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动,设点
移动,设点![]() 、
、![]() 移动的时间为
移动的时间为![]() 秒.
秒.

![]() 求点
求点![]() 的坐标;
的坐标;
![]() 当
当![]() 为何值时,
为何值时,![]() 的面积为
的面积为![]() 个平方单位?
个平方单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() ,∠DAB=∠DCB,对角线
,∠DAB=∠DCB,对角线![]() ,
,![]() 交于点
交于点![]() .分别添加下列条件之一:①
.分别添加下列条件之一:①![]() ;②
;②![]() ;③
;③![]() ;④∠ABC=∠ADC,能使四边形
;④∠ABC=∠ADC,能使四边形![]() 成为平行四边形,则正确的选项有_____.(填写序号)
成为平行四边形,则正确的选项有_____.(填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于给定的一次函数y=ax+b(a≠0),把形如![]() 的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
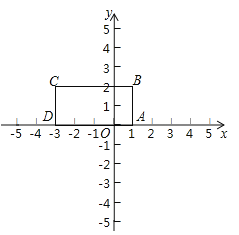
(1)已知函数y=2x+l.
①若点P(-1,m)在这个一次函数的衍生函数图像上,则m= .
②这个一次函数的衍生函数图像与矩形ABCD的边的交点坐标分别为 .
(2)当函数y=kx-3(k>0)的衍生函数的图象与矩形ABCD有2个交点时,k的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①b<0;②4a+2b+c<0;③a﹣b+c>0;④(a+c)2<b2.其中正确的结论是
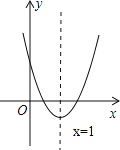
A.①② B.①③ C.①③④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E.
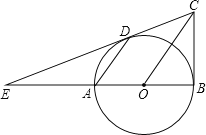
(1)求证:直线CD是⊙O的切线;
(2)若DE=2BC,求AD:OC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△OBC的顶点分别为O(0,0),B(3,﹣1)、C(2,1).
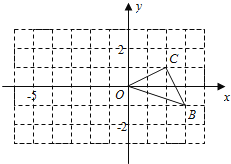
(1)以点O(0,0)为位似中心,按比例尺2:1在位似中心的异侧将△OBC放大为△OB′C′,放大后点B、C两点的对应点分别为B′、C′,画出△OB′C′,并写出点B′、C′的坐标:B′( , ),C′( , );
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点M′的坐标( , ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com