
【题目】如图,已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E.
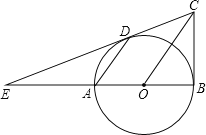
(1)求证:直线CD是⊙O的切线;
(2)若DE=2BC,求AD:OC的值.
【答案】(1)见解析(2)2:3
【解析】解:(1)证明:连接DO,
∵AD∥OC,∴∠DAO=∠COB,∠ADO=∠COD。
又∵OA=OD,∴∠DAO=∠ADO。
∴∠COD=∠COB。
在△COD和△COB中,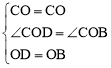 ,
,
∴△COD≌△COB(SAS)。
∴∠CDO=∠CBO=90°.
又∵点D在⊙O上,∴CD是⊙O的切线.

(2)∵△COD≌△COB.∴CD=CB。
∵DE=2BC,∴ED=2CD。
∵AD∥OC,∴△EDA∽△ECO。
∴AD:OC=DE:CE=2:3。
(1)连接OD,易证得△COD≌△COB(SAS),然后由全等三角形的对应角相等,求得∠CDO=90°,即可证得直线CD是⊙O的切线。
(2)由△COD≌△COB.可得CD=CB,即可得DE=2CD,易证得△EDA∽△ECO,然后由相似三角形的对应边成比例,求得AD:OC的值。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)若x1,x2是原方程的两根,且![]() ,求m的值,并求出此时方程的两根.
,求m的值,并求出此时方程的两根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:
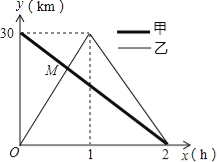
(1)写出A、B两地直接的距离;
(2)求出点M的坐标,并解释该点坐标所表示的实际意义;
(3)若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.已知:如图1,直线l及直线l外一点A.
求作:直线AD,使得AD∥l.作法:如图2,
①在直线l上任取一点B,连接AB;
②以点B为圆心,AB长为半径画弧,
交直线l于点C;
③分别以点A,C为圆心,AB长为半径
画弧,两弧交于点D(不与点B重合);
④作直线AD.
所以直线AD就是所求作的直线.根据小东设计的尺规作图过程,完成下面的证明.(说明:括号里填推理的依据)
证明:连接CD.
∵AD=CD=__________=__________,
∴四边形ABCD是 ( ).
∴AD∥l( ).
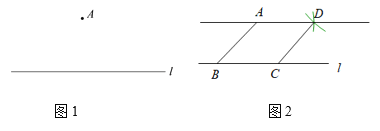
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解初中阶段女生身高情况,从某中学初二年级120名女生中随意抽出40名同龄女生的身高数据,经过分组整理后的频数分布表及频数分布直方图如图所示:
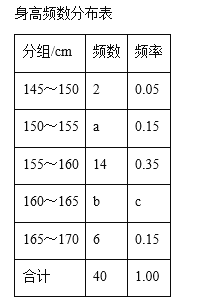
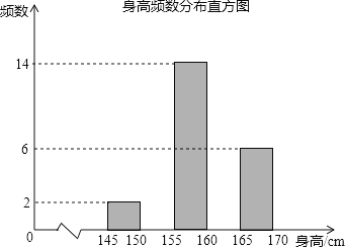
结合以上信息,回答问题:
(1)a=______,b=______,c=______.
(2)请你补全频数分布直方图.
(3)试估计该年级女同学中身高在160~165cm的同学约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() .点
.点![]() 在
在![]() 上以
上以![]() 的速度由点
的速度由点![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 在
在![]() 上由点
上由点![]() 向点
向点![]() 运动,它们运动的时间为
运动,它们运动的时间为![]() .
.
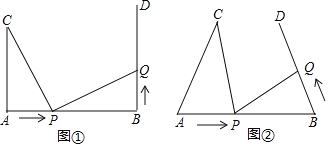
(1)如图①,![]() ,
,![]() ,若点
,若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,当
的运动速度相等,当![]() 时,
时,![]() 与
与![]() 是否全等,请说明理由,并判断此时线段
是否全等,请说明理由,并判断此时线段![]() 和线段
和线段![]() 的位置关系;
的位置关系;
(2)如图②,将图①中的“![]() ,
,![]() ”为改“
”为改“![]() ”,其他条件不变.设点
”,其他条件不变.设点![]() 的运动速度为
的运动速度为![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 与
与![]() 全等?若存在,求出相应的
全等?若存在,求出相应的![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .
与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com