
°æƒø°ø‘⁄“ªÃı± ÷±µƒπ´¬∑…œ”–A°¢B¡Ωµÿ£¨º◊∆Ô◊‘––≥µ¥”AµÿµΩBµÿ£ª““∆Ô◊‘––≥µ¥”BµÿµΩAµÿ£¨µΩ¥ÔAµÿ∫Û¡¢º¥∞¥‘≠¬∑∑µªÿ£¨»ÁÕº «º◊°¢““¡Ω»À¿ÎBµÿµƒæý¿Îy£®km£©”Ζ– ª ±x£®h£©÷ƺ‰µƒ∫Ø ˝ÕºœÛ£¨∏˘æðÕºœÛΩ‚¥“‘œ¬Œ £∫
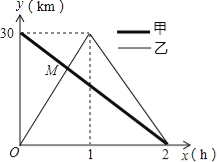
£®1£©–¥≥ˆA°¢B¡Ωµÿ÷±Ω”µƒæý¿Î£ª
£®2£©«Û≥ˆµ„Mµƒ◊¯±Í£¨≤¢Ω‚ Õ∏√µ„◊¯±ÍÀ˘±Ì 浃 µº “‚“£ª
£®3£©»Ù¡Ω»À÷ƺ‰±£≥÷µƒæý¿Î≤ª≥¨π˝3km ±£¨ƒÐπª”√ŒÞœþ∂‘Ω≤ª˙±£≥÷¡™œµ£¨«Î÷±Ω”–¥≥ˆº◊°¢““¡Ω»ÀƒÐπª”√ŒÞœþ∂‘Ω≤ª˙±£≥÷¡™œµ ±xµƒ»°÷µ∑∂Œß£Æ
°æ¥∞∏°ø£®1£©30«ß√◊£ª£®2£©µ„Mµƒ◊¯±ÍŒ™£®![]() £¨20£©£¨±Ì æ
£¨20£©£¨±Ì æ![]() –° ±∫Û¡Ω≥µœý”ˆ£¨¥À ±æý¿ÎBµÿ20«ß√◊£ª£®3£©µ±
–° ±∫Û¡Ω≥µœý”ˆ£¨¥À ±æý¿ÎBµÿ20«ß√◊£ª£®3£©µ±![]() °Ðx°Ð
°Ðx°Ð![]() ªÚ
ªÚ![]() °Ðx°Ð2 ±£¨º◊°¢““¡Ω»ÀƒÐπª”√ŒÞœþ∂‘Ω≤ª˙±£≥÷¡™œµ£Æ
°Ðx°Ð2 ±£¨º◊°¢““¡Ω»ÀƒÐπª”√ŒÞœþ∂‘Ω≤ª˙±£≥÷¡™œµ£Æ
°æΩ‚Œˆ°ø
£®1£©x=0 ±º◊µƒy÷µº¥Œ™A°¢B¡Ωµÿµƒæý¿Î£ª
£®2£©∏˘æðÕºœÛ«Û≥ˆº◊°¢““¡Ω»ÀµƒÀŸ∂»£¨‘Ÿ¿˚”√œý”ˆŒ «Û≥ˆœý”ˆ ±º‰£¨»ª∫Û«Û≥ˆ““µƒ¬∑≥ú¥ø…µ√µΩµ„Mµƒ◊¯±Í“‘º∞ µº “‚“£ª
£®3£©∑÷œý”ˆ«∞∫Õœý”ˆ∫Û¡Ω÷÷«Èøˆ«Û≥ˆxµƒ÷µ£¨‘Ÿ«Û≥ˆ◊Ó∫Û¡Ω»À∂ºµΩ¥ÔBµÿ«∞¡Ω»Àœýæý3«ß√◊µƒ ±º‰£¨»ª∫Û–¥≥ˆ¡Ω∏ˆ»°÷µ∑∂Œßº¥ø…£Æ
Ω‚£∫£®1£©°þx=0 ±£¨º◊æý¿ÎBµÿ30«ß√◊£¨
°ýA°¢B¡Ωµÿµƒæý¿ÎŒ™30«ß√◊£Æ
£®2£©”…Õºø…÷™£¨º◊µƒÀŸ∂»£∫30°¬2=15«ß√◊/ ±£¨““µƒÀŸ∂»£∫30°¬1=30«ß√◊/ ±£¨
30°¬£®15+30£©=![]() £¨
£¨![]() °¡30=20«ß√◊£Æ
°¡30=20«ß√◊£Æ
°ýµ„Mµƒ◊¯±ÍŒ™£®![]() £¨20£©£¨±Ì æ
£¨20£©£¨±Ì æ![]() –° ±∫Û¡Ω≥µœý”ˆ£¨¥À ±æý¿ÎBµÿ20«ß√◊£Æ
–° ±∫Û¡Ω≥µœý”ˆ£¨¥À ±æý¿ÎBµÿ20«ß√◊£Æ
£®3£©…Ëx–° ± ±£¨º◊°¢““¡Ω»Àœýæý3km£¨
¢Ÿ»Ù «œý”ˆ«∞£¨‘Ú15x+30x=30©Å3£¨Ω‚µ√x=![]() £Æ
£Æ
¢⁄»Ù «œý”ˆ∫Û£¨‘Ú15x+30x=30+3£¨Ω‚µ√x=![]() £Æ
£Æ
¢€»Ù «µΩ¥ÔBµÿ«∞£¨‘Ú15x©Å30£®x©Å1£©=3£¨Ω‚µ√x=![]() £Æ
£Æ
°ýµ±![]() °Ðx°Ð
°Ðx°Ð![]() ªÚ
ªÚ![]() °Ðx°Ð2 ±£¨º◊°¢““¡Ω»ÀƒÐπª”√ŒÞœþ∂‘Ω≤ª˙±£≥÷¡™œµ£Æ
°Ðx°Ð2 ±£¨º◊°¢““¡Ω»ÀƒÐπª”√ŒÞœþ∂‘Ω≤ª˙±£≥÷¡™œµ£Æ


 –°Ã‚øÒ◊ˆœµ¡–¥∞∏
–°Ã‚øÒ◊ˆœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
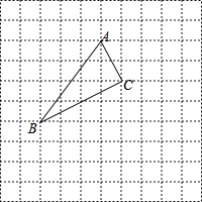
°æƒø°ø »ÁÕº£¨∞—°˜ABC∑≈÷√‘⁄√ø∏ˆ–°’˝∑Ω–Œ±þ≥§Œ™1µƒÕ¯∏Ò÷–£¨µ„A£¨B£¨Cæ˘‘⁄∏Òµ„…œ£¨Ω®¡¢ µ±µƒ∆Ω√Ê÷±Ω«◊¯±ÍœµxOy£¨ πµ„A£®1£¨4£©£¨°˜ABC”ΰ˜A'B'C'πÿ”⁄y÷·∂‘≥∆£Æ
£®1£©ª≠≥ˆ∏√∆Ω√Ê÷±Ω«◊¯±Íœµ”ΰ˜A'B'C'£ª
£®2£©‘⁄y÷·…œ’“µ„P£¨ πPC+PB'µƒ÷µ◊Ó–°£¨«Ûµ„Pµƒ◊¯±Í”ÎPC+PB'µƒ◊Ó–°÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø¥∫Ω⁄«∞–°Õıª®1200‘™¥”≈©√≥ –≥°π∫Ω¯≈˙∑¢º€∑÷±Œ™√øœ‰30‘™”Î50‘™µƒA,B¡Ω÷÷ÀÆπ˚Ω¯––œ˙ €£¨≤¢∑÷±“‘√øœ‰35‘™”Î60‘™µƒº€∏Ò≥ˆ €£¨…Ëπ∫Ω¯AÀÆπ˚xœ‰£¨BÀÆπ˚yœ‰.
(1)»√–°ÕıΩ´ÀÆπ˚»´≤ø €≥ˆπ≤◊¨¡À215‘™£¨‘Ú–°Õıπ≤π∫Ω¯A°¢BÀÆπ˚∏˜∂ý…Ÿœ‰?
(2)»Ù“™«Ûπ∫Ω¯AÀÆπ˚µƒ ˝¡ø≤ªµ√…Ÿ”⁄BÀÆπ˚µƒ ˝¡ø£¨‘Ú”¶∏√»Á∫Œ∑÷≈‰π∫Ω¯A, BÀÆπ˚µƒ ˝¡ø≤¢»´≤ø €≥ˆ≤≈ƒÐªÒµ√◊Ó¥Û¿˚»Û£¨¥À ±◊Ó¥Û¿˚»Û «∂ý…Ÿ?
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£Àʪ˙≥È»°≤ø∑÷—ß…˙£¨∂‘°∞—ßœ∞œ∞πþ°±Ω¯––Œ æ̵˜≤È£Æ
…˺∆µƒŒ £∫∂‘◊‘º∫◊ˆ¥ÌµƒÃ‚ƒøΩ¯––’˚¿Ì°¢∑÷Œˆ°¢∏ƒ’˝£ª
¥∞∏—°œÓŒ™£∫A£∫∫Ð…Ÿ£¨B£∫”– ±£¨C£∫≥£≥££¨D£∫◊Ð «£ª
Ω´µ˜≤ÈΩ·π˚µƒ ˝æðΩ¯––¡À’˚¿Ì°¢ªÊ÷∆≥…≤ø∑÷Õ≥º∆Õº»Áœ¬£∫
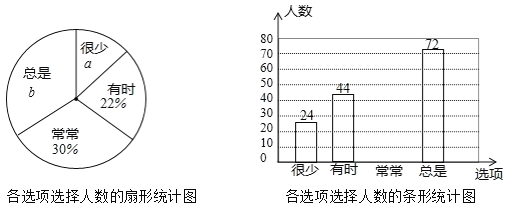
«Î∏˘æðÕº÷––≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
£®1£©∏√µ˜≤ȵƒ—˘±æ»ð¡øŒ™ £¨a= %£¨b= %£¨°∞≥£≥£°±∂‘”¶…»–Œµƒ‘≤–ƒΩ«Œ™ £ª
£®2£©«Îƒ„≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®3£©»Ù∏√–£”–3200√˚—ß…˙£¨«Îƒ„π¿º∆∆‰÷–°∞≥£≥£°±∫Õ°∞◊Ð «°±∂‘¥ÌÃ‚Ω¯––’˚¿Ì°¢∑÷Œˆ°¢∏ƒ’˝µƒ—ß…˙∏˜”–∂ý…Ÿ√˚£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
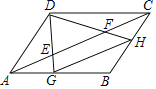
°æƒø°ø»ÁÕº£¨E£¨F «∆Ω––Àƒ±þ–ŒABCD∂‘Ω«œþAC…œ¡Ωµ„£¨AE=CF=![]() AC£Æ¡¨Ω”DE£¨DF≤¢—”≥§£¨∑÷±ΩªAB£¨BC”⁄µ„G£¨H£¨¡¨Ω”GH£¨‘Ú
AC£Æ¡¨Ω”DE£¨DF≤¢—”≥§£¨∑÷±ΩªAB£¨BC”⁄µ„G£¨H£¨¡¨Ω”GH£¨‘Ú![]() µƒ÷µŒ™£®°°°°£©
µƒ÷µŒ™£®°°°°£©
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£Œ™¡ÀΩ‚—ß…˙µƒ∞≤»´“‚ ∂«Èøˆ£¨‘⁄»´–£∑∂Œßƒ⁄Àʪ˙≥È»°≤ø∑÷—ß…˙Ω¯––Œ æ̵˜≤È£¨∏˘æð≤ÈΩ·π˚£¨∞——ß…˙µƒ∞≤»´“‚ ∂∑÷≥…µ≠±°°¢“ª∞„°¢Ωœ«ø°¢∫ЫøÀƒ∏ˆ≤„¥Œ£¨≤¢ªÊ÷∆≥…»Áœ¬¡Ω∑˘…–≤ªÕÍ’˚µƒÕ≥º∆Õº£∫

∏˘æð“‘…œ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
£®1£©∏√–£”–1200√˚—ß…˙£¨œ÷“™∂‘∞≤»´“‚ ∂Œ™µ≠±°°¢“ª∞„µƒ—ß…˙«øªØ∞≤»´ΩÔ˝£¨∏˘æðµ˜≤ÈΩ·π˚£¨π¿º∆»´–£–Ë“™«øªØ∞≤»´ΩÔ˝µƒ—ß…˙‘º”–∂ý…Ÿ√˚£ø
£®2£©«ÎΩ´Ãı–ŒÕ≥º∆Õº≤π≥‰ÕÍ’˚£Æ
£®3£©«Û≥ˆ∞≤»´“‚ ∂Œ™°∞Ωœ«ø°±µƒ—ß…˙À˘’ºµƒ∞Ÿ∑÷±»£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄»ÒΩ«»˝Ω«–ŒABC÷–£¨µ„D£¨E∑÷±‘⁄±þAC£¨AB…œ£¨AG°ÕBC”⁄µ„G£¨AF°ÕDE”⁄µ„F£¨°œEAF=°œGAC£Æ
£®1£©«Û÷§£∫°˜ADE°◊°˜ABC£ª
£®2£©»ÙAD=3£¨AB=5£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™AB «°—Oµƒ÷±æ∂£¨BC°ÕAB£¨¡¨Ω·OC£¨œ“AD°ŒOC£¨÷±œþCDΩªBAµƒ—”≥§œþ”⁄µ„E£Æ
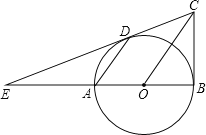
£®1£©«Û÷§£∫÷±œþCD «°—Oµƒ«–œþ£ª
£®2£©»ÙDE=2BC£¨«ÛAD£∫OCµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºµ„E£¨F∑÷± «æÿ–ŒABCDµƒ±þAD£¨AB…œ“ªµ„£¨»ÙAE=DC=2ED£¨«“EF°ÕEC£Æ
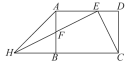
£®1£©«Û÷§£∫µ„FŒ™ABµƒ÷–µ„£Æ
£®2£©—”≥§EF”ÎCBµƒ—”≥§œþœýΩª”⁄µ„H£¨¡¨Ω”AH£¨“—÷™ED=2£¨«ÛAHµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com