
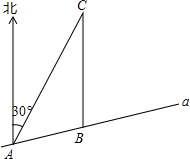
 如图,某市郊景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东30°方向,位于景点B的正北方向,且景点B位于景点A的北偏东75°方向,景点B与景点A距离为4km.
如图,某市郊景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东30°方向,位于景点B的正北方向,且景点B位于景点A的北偏东75°方向,景点B与景点A距离为4km.分析 (1)过点B作BD⊥AC于点D,先解Rt△ADB,得出AD=BD=2$\sqrt{2}$km,再解Rt△CBD,得出CD=2$\sqrt{6}$km,则AC=AD+CD;
(2)过点C作CE⊥AB于点E.解等腰直角△ACE,即可求出CE的长.
解答 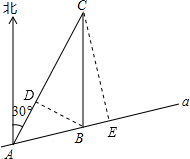 解:(1)如图,过点B作BD⊥AC于点D.
解:(1)如图,过点B作BD⊥AC于点D.
在Rt△ADB中,∵∠ADB=90°,∠BAD=75°-30°=45°,AB=4km,
∴AD=BD=$\frac{\sqrt{2}}{2}$AB=2$\sqrt{2}$km.
在Rt△CBD中,∵∠CDB=90°,∠BCD=30°,
∴CD=$\sqrt{3}$BD=2$\sqrt{6}$km,
∴AC=AD+CD=(2$\sqrt{2}$+2$\sqrt{6}$)km;
答:景点A与景点C的距离为(2$\sqrt{2}$+2$\sqrt{6}$)km;
(2)过点C作CE⊥AB于点E.
在Rt△ACE中,∵∠AEC=90°,∠CAE=45°,AC=(2$\sqrt{2}$+2$\sqrt{6}$)km,
∴CE=$\frac{\sqrt{2}}{2}$AC=(2+2$\sqrt{3}$)km.
答:这条公路长为(2+2$\sqrt{3}$)km.
点评 本题主要考查解直角三角形的应用-方向角问题,准确作出辅助线构造直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
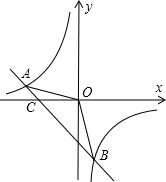 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
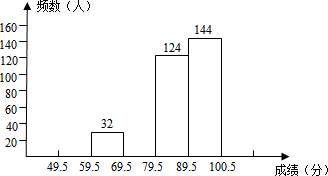 某县九年级有15000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分(得分取正整数,满分100分)进行统计:
某县九年级有15000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分(得分取正整数,满分100分)进行统计:| 分 组 | 频 数 | 频 率 |
| 49.5~59.5 | 20 | b |
| 59.5~69.5 | 32 | 0.08 |
| 69.5~79.5 | a | 0.20 |
| 79.5~89.5 | 124 | c |
| 89.5~100.5 | 144 | 0.36 |
| 合 计 | 400 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com