
【题目】已知,数轴上点![]() 在原点左边,到原点的距离为8个单位长度,点
在原点左边,到原点的距离为8个单位长度,点![]() 在原点的右边,从点
在原点的右边,从点![]() 走到点
走到点![]() ,要经过32个单位长度.
,要经过32个单位长度.
(1)求![]() 、
、![]() 两点所对应的数;
两点所对应的数;
(2)若点![]() 也是数轴上的点,点
也是数轴上的点,点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到原点的距离的3倍,求点
到原点的距离的3倍,求点![]() 对应的数;
对应的数;
(3)已知,点![]() 从点
从点![]() 向右出发,速度为每秒1个单位长度,同时点
向右出发,速度为每秒1个单位长度,同时点![]() 从点
从点![]() 向右出发,速度为每秒2个单位长度,若点
向右出发,速度为每秒2个单位长度,若点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到原点
到原点![]() 距离相等,则点
距离相等,则点![]() 到原点
到原点![]() 距离与点
距离与点![]() 到点
到点![]() 的距离与值是否变化?若不变,求其值.
的距离与值是否变化?若不变,求其值.
【答案】(1)点![]() 表示-8,点
表示-8,点![]() 表示24;(2)
表示24;(2)![]() 或
或![]() ;(3)
;(3)![]() 的值没有变化,为12.
的值没有变化,为12.
【解析】
(1)直接根据实数与数轴上各点的对应关系求出A,B表示的数即可;
(2)设点C表示的数为c,再根据点C到点B的距离是点C到原点的距离的3倍列出关于c的方程,求出c的值即可;
(3)设运动时间为t秒,则AM=t,NO=24+2t,再根据点P是NO的中点用t表示出PO的长,再求出PO-AM的值即可.
(1)∵数轴上点![]() 在原左边,到原点的距离为8个单位长度,点
在原左边,到原点的距离为8个单位长度,点![]() 在原点的右边,从点
在原点的右边,从点![]() 走到点
走到点![]() ,要经过32个单位长度.
,要经过32个单位长度.
∴点![]() 表示-8,点
表示-8,点![]() 表示24;
表示24;
(2)设点![]() 表示的数为
表示的数为![]()
∵点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到原点的距离的3倍
到原点的距离的3倍
∴![]()
∴![]() 或
或![]() ,解得
,解得![]() 或
或![]()
(3)不变化
设运动时间为![]() 秒,则
秒,则![]() ,
,![]()
∵点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到原点
到原点![]() 距离相等
距离相等
∴点![]() 是
是![]() 的中点
的中点
∴![]()
∴![]()
∴![]() 的值没有变化.
的值没有变化.


科目:初中数学 来源: 题型:
【题目】利用图形面积可以解释代数恒等式的正确性,也可以解释不等式的正确性.
(1)根据下列所示图形写出一个代数恒等式 .
(2)已知正数a,b,c和m,n,l,满足ambnclk,试构造边长为k的正方形,利用图形面积来说明albmcnk2.
思考过程如下:
因为ambnclk,所以a,b,c,m,n,l,均 k(填“大于”或“小于”).由于k2可以看成一个正方形的面积,则al、bm、cn可以分别看成三个长方形的面积.请画出图形,并利用图形面积来说明albmcnk2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:射线OC在∠AOB的外部,如图,∠AOB=90°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.
(1)请在图中补全图形;
(2)求∠MON的度数.
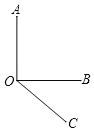
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在桌面上,有若千个完全相同的小正方体堆成的一个几何体![]() ,每个小正方体的边长为
,每个小正方体的边长为![]() ,如图所示.
,如图所示.
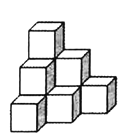
![]() 请画出这个几何体
请画出这个几何体![]() 的三视图. (用黑色水笔描清楚);
的三视图. (用黑色水笔描清楚);
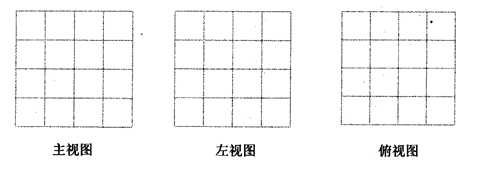
![]() 若将此几何体
若将此几何体![]() 的表面喷上红漆(放在桌面上的一面不喷),则几何体
的表面喷上红漆(放在桌面上的一面不喷),则几何体![]() 上喷上红漆的面积为
上喷上红漆的面积为 ![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
![]() 若现在你的手头还有这样的一些边长为
若现在你的手头还有这样的一些边长为![]() 的小正方体可添放在几何体
的小正方体可添放在几何体![]() 上,要保持主视图和左视图不变,则最多可以添加 个小正方体.
上,要保持主视图和左视图不变,则最多可以添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七、八年级各有学生400人,为了解这两个年级普及安全教育的情况,进行了抽样调查,过程如下
选择样本,收集数据从七、八年级各随机抽取20名学生,进行安全教育考试,测试成绩(百分制)如下:
七年级 85 79 89 83 89 98 68 89 79 59
99 87 85 89 97 86 89 90 89 77
八年级 71 94 87 92 55 94 98 78 86 94
62 99 94 51 88 97 94 98 85 91
分组整理,描述数据
(1)按如下频数分布直方图整理、描述这两组样本数据,请补全八年级20名学生安全教育频数分布直方图;

(2)两组样本数据的平均数、中位数、众数、优秀率如下表所示,请补充完整;

得出结论,说明理由.
(3)整体成绩较好的年级为___,理由为___(至少从两个不同的角度说明合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1930年,德国汉堡大学的学生考拉兹,曾经提出过这样一个数学猜想:对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能够得到1.这一猜想后来成为著名的“考拉兹猜想”,又称“奇偶归一猜想”.虽然这个结论在数学上还没有得到证明,但举例验证都是正确的,例如:取正整数5,最少经过下面5步运算可得1,即:![]() 如果正整数
如果正整数![]() 最少经过6步运算可得到1,则
最少经过6步运算可得到1,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com