
����Ŀ������ͼ��������Խ��ʹ������ʽ����ȷ�ԣ�Ҳ���Խ��Ͳ���ʽ����ȷ�ԣ�
��1������������ʾͼ��д��һ���������ʽ ��
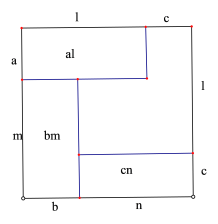
��2����֪����a��b��c��m��n��l������ambnclk���Թ���߳�Ϊk�������Σ�����ͼ�������˵��albmcnk2��
˼���������£�
��Ϊambnclk������a��b��c��m��n��l���� k����������������С������������k2���Կ���һ�������ε��������al��bm��cn���Էֱ����������ε�������뻭��ͼ�Σ�������ͼ�������˵��albmcnk2��

���𰸡���1��![]() ����2��С�ڣ����ɼ���⣮
����2��С�ڣ����ɼ���⣮
��������
��1���ȷֱ��ʾ���������ε����Ϊ![]() ��С���������Ϊ
��С���������Ϊ![]() ����Ӱ�������Ϊ
����Ӱ�������Ϊ![]() ���ٸ���С�����ε����+4�������ε����=����������������ɵõ��𰸣�
���ٸ���С�����ε����+4�������ε����=����������������ɵõ��𰸣�
��2����������ָ�����������Σ�ʹ��߳�����ambnclk����a��b��c��m��n��l�����������������б߳�Ϊa��l��b��m��c��n�ij����Σ�����ͨ�������Σ����ɵõ�albmcnk2��
��1����С�����ε����+4�������ε����=�������������
��![]() ��
��
�ʴ��ǣ�![]() ��
��
��2������һ���߳�Ϊk�������Σ���ͼ��ʾ����Ȼ���㣺ambnclk��
����ͼ�ο�֪���������ڲ�3�������ε����֮��С�������ε����������albmcnk2��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
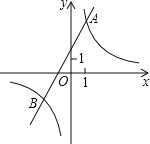
����Ŀ����ͼ����֪����������y1��![]() ��ͼ����һ�κ�����y2��ax+b��ͼ���ཻ�ڵ�A��1��4����B��m����2��
��ͼ����һ�κ�����y2��ax+b��ͼ���ཻ�ڵ�A��1��4����B��m����2��
��1�����������������һ�κ����Ĺ�ϵʽ��
��2���۲�ͼ��ֱ��д��ʹ��y1��y2�������Ա���x��ȡֵ��Χ��
��3�������C��x���ϵĵ㣬����ABC��������Ϊ6�����C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
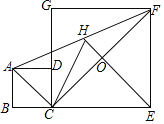
����Ŀ����ͼ��������ABCD��������CEFC�У���D��CG�ϣ�BC��1��CE��3��H��AF���е㣬EH��CF���ڵ�O��
��1����֤��HC��HF��
��2����HE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
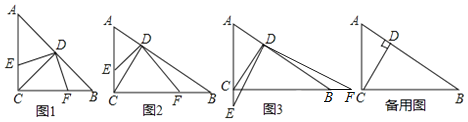
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() �ڵ�D����E��ֱ��AC��һ���㣬����DE������D��
�ڵ�D����E��ֱ��AC��һ���㣬����DE������D��![]() ����ֱ��BC�ڵ�F��
����ֱ��BC�ڵ�F��
![]() ̽�����֣�
̽�����֣�
��ͼ1����![]() ����E���߶�AC�ϣ���
����E���߶�AC�ϣ���![]() ______��
______��
![]() ��ѧ˼����
��ѧ˼����
![]() ��ͼ2������E���߶�AC�ϣ���
��ͼ2������E���߶�AC�ϣ���![]() ______
______![]() �ú�m��n�Ĵ���ʽ��ʾ
�ú�m��n�Ĵ���ʽ��ʾ![]() ��
��
![]() ����E��ֱ��AC���˶�ʱ��
����E��ֱ��AC���˶�ʱ��![]() �еĽ����Ƿ���Ȼ�����������ͼ3�����θ���֤����
�еĽ����Ƿ���Ȼ�����������ͼ3�����θ���֤����
![]() ��չӦ�ã���
��չӦ�ã���![]() ��
��![]() ��
��![]() ����ֱ��д��CE�ij���
����ֱ��д��CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+��2k+1��x+k2=0������������ȵ�ʵ������
��1����k��ȡֵ��Χ��
��2���跽�̢ٵ�����ʵ�����ֱ�Ϊx1��x2����k=1ʱ����x12+x22��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1��ACƽ��DAB��12����˵��AB��CD��λ�ù�ϵ��������֤����
��2����ͼ2���ڣ�1���Ľ����£�AB���·���P����ABP30��G��CD����һ�㣬PQƽ��BPG��PQ��GN��GMƽ��DGP�����н��ۣ�
��DGPMGN��ֵ���䣻
��MGN�Ķ������䣮
����֤����ֻ��һ������ȷ�ģ�����������ȷ��ѡ����ֵ��
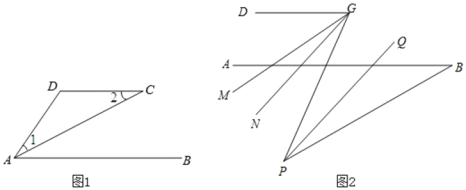
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ���˽�����꼶1000��ѧ�������彡��������Ӹ��꼶�����ȡ��������ѧ���������ǰ����أ���Ϊ��������λ��kg���ֳ����飨A��39.5��46��B��46.5��53.5��C��53.5��60.5��D��60.5��67.5��E��67.5��74.5����������ͳ�����ݻ��������������в�������ͳ��ͼ������������⣮
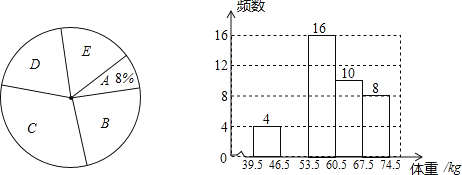
��1�����һ����ȡ���� ����ѧ��������ȫƵ��ֱ��ͼ��
��2��C��ѧ����������ռ�İٷֱ�Ϊ�� ����
��3��������ͳ��ͼ��D���Բ�Ľ����� ���ȣ�
��4��������Ƹ�У�����꼶���س���60kg��ѧ����Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪��ABC��AB=AC���Ա�ABΪֱ������O��BC�ڵ�D����AC�ڵ�E������DE��
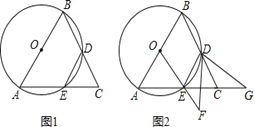
��1����֤��DE=DC��
��2����ͼ2������OE������EDC�Ƶ�D��ʱ����ת��ʹ��EDC�����߷ֱ�OE���ӳ����ڵ�F��AC���ӳ����ڵ�G����̽���߶�DF��DG��������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�������ϵ�![]() ��ԭ����ߣ���ԭ��ľ���Ϊ8����λ���ȣ���
��ԭ����ߣ���ԭ��ľ���Ϊ8����λ���ȣ���![]() ��ԭ����ұߣ��ӵ�
��ԭ����ұߣ��ӵ�![]() �ߵ���
�ߵ���![]() ��Ҫ����32����λ���ȣ�
��Ҫ����32����λ���ȣ�
��1����![]() ��
��![]() ��������Ӧ������
��������Ӧ������
��2������![]() Ҳ�������ϵĵ㣬��
Ҳ�������ϵĵ㣬��![]() ����
����![]() �ľ����ǵ�
�ľ����ǵ�![]() ��ԭ��ľ����3�������
��ԭ��ľ����3�������![]() ��Ӧ������
��Ӧ������
��3����֪����![]() �ӵ�
�ӵ�![]() ���ҳ������ٶ�Ϊÿ��1����λ���ȣ�ͬʱ��
���ҳ������ٶ�Ϊÿ��1����λ���ȣ�ͬʱ��![]() �ӵ�
�ӵ�![]() ���ҳ������ٶ�Ϊÿ��2����λ���ȣ�����
���ҳ������ٶ�Ϊÿ��2����λ���ȣ�����![]() ����
����![]() �ľ������
�ľ������![]() ��ԭ��
��ԭ��![]() ������ȣ����
������ȣ����![]() ��ԭ��
��ԭ��![]() �������
�������![]() ����
����![]() �ľ�����ֵ�Ƿ�仯�������䣬����ֵ��
�ľ�����ֵ�Ƿ�仯�������䣬����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com