
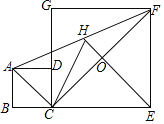
【题目】如图,正方形ABCD和正方形CEFC中,点D在CG上,BC=1,CE=3,H是AF的中点,EH与CF交于点O.
(1)求证:HC=HF.
(2)求HE的长.
【答案】(1)见解析;(2)HE=![]() .
.
【解析】
(1)利用直角三角形斜边上的中线等于斜边的一半求解即可;
(2)分别求得HO和OE的长后即可求得HE的长.
(1)证明:∵AC、CF分别是正方形ABCD和正方形CGFE的对角线,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
又∵H是AF的中点,
∴CH=HF;
(2)∵CH=HF,EC=EF,
∴点H和点E都在线段CF的中垂线上,
∴HE是CF的中垂线,
∴点H和点O是线段AF和CF的中点,
∴OH=![]() AC,
AC,
在Rt△ACD和Rt△CEF中,AD=DC=1,CE=EF=3,
∴AC=![]() ,
,
∴CF=3![]() ,
,
又OE是等腰直角△CEF斜边上的高,
∴OE=![]() ,
,
∴HE=HO+OE=2![]() ;
;


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
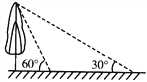
【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l为x+y=8,点P(x,y)在l上且x>0,y>0,点A的坐标为(6,0).
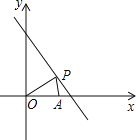
(1)设△OPA的面积为S,求S与x的函数关系式,并直接写出x的取值范围;
(2)当S=9时,求点P的坐标;
(3)在直线l上有一点M,使OM+MA的和最小,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
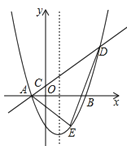
【题目】如图,在平面直角坐标系中,抛物线y=ax2-2ax-3a(a>0)与x轴交于A,B两点(点A在点B左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)求点A的坐标及直线l的函数表达式(其中k,b用含a的式子表示);
(2)点E为直线l下方抛物线上一点,当△ADE的面积的最大值为![]() 时,求抛物线的函数表达式.
时,求抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在开学前去商场购进A、B两种品牌的足球,购买A品牌足球共花费3000元,购买B品牌足球共花费1600元,且购买A品牌足球数量是购买B品牌足球的3倍,已知购买一个B品牌足球比购买一个A品牌足球多花30元.(1)求购买一个A品牌、一个B品牌足球各需多少元?
(2)为了进一步发展“校园足球”,学校在开学后再次购进了A、B两种品牌的足球,每种品牌的足球不少于15个,总花费恰好为2268元,且在购买时,商场对两种品牌的足球的销售单价进行了调整,A品牌足球销售单价比第一次购买时提高了8%,B品牌足球按第一次购买时销售单价的9折出售.那么此次有哪些购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用图形面积可以解释代数恒等式的正确性,也可以解释不等式的正确性.
(1)根据下列所示图形写出一个代数恒等式 .
(2)已知正数a,b,c和m,n,l,满足ambnclk,试构造边长为k的正方形,利用图形面积来说明albmcnk2.
思考过程如下:
因为ambnclk,所以a,b,c,m,n,l,均 k(填“大于”或“小于”).由于k2可以看成一个正方形的面积,则al、bm、cn可以分别看成三个长方形的面积.请画出图形,并利用图形面积来说明albmcnk2.

查看答案和解析>>
科目:初中数学 来源: 题型:
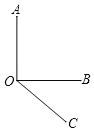
【题目】已知:射线OC在∠AOB的外部,如图,∠AOB=90°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.
(1)请在图中补全图形;
(2)求∠MON的度数.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com