
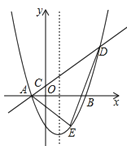
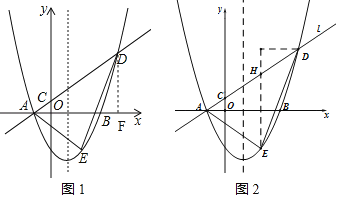
【题目】如图,在平面直角坐标系中,抛物线y=ax2-2ax-3a(a>0)与x轴交于A,B两点(点A在点B左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)求点A的坐标及直线l的函数表达式(其中k,b用含a的式子表示);
(2)点E为直线l下方抛物线上一点,当△ADE的面积的最大值为![]() 时,求抛物线的函数表达式.
时,求抛物线的函数表达式.
【答案】(1)A(-1,0),y=ax+a;(2)y=![]() x2-
x2-![]() x-
x-![]() .
.
【解析】分析:(1)由抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于两点A、B,求得A点的坐标,作DF⊥x轴于F,根据平行线分线段成比例定理求得D的坐标,然后利用待定系数法法即可求得直线l的函数表达式.
(2)设点E(m,ax2﹣2ax﹣3a),知HE=(ax+a)﹣(ax2﹣2ax﹣3a)=﹣ax2+3ax+4a,根据直线和抛物线解析式求得点D的横坐标,由S△ADE=S△AEH+S△DEH列出函数解析式,根据最值确定a的值即可.
详解:(1)令y=0,则ax2﹣2ax﹣3a=0,解得:x1=﹣1,x2=3.
∵点A在点B的左侧,∴A(﹣1,0),如图1,作DF⊥x轴于F,
∴DF∥OC,∴![]() =
=![]() .
.
∵CD=4AC,∴![]() =
=![]() =4.
=4.
∵OA=1,∴OF=4,∴D点的横坐标为4,代入y=ax2﹣2ax﹣3a得:y=5a,∴D(4,5a),把A、D坐标代入y=kx+b得![]() ,解得:
,解得: ![]() ,∴直线l的函数表达式为y=ax+a.
,∴直线l的函数表达式为y=ax+a.
(2)如图2,过点E作EH∥y轴,交直线l于点H,
设E(x,ax2﹣2ax﹣3a),则H(x,ax+a),∴HE=(ax+a)﹣(ax2﹣2ax﹣3a)=﹣ax2+3ax+4a,由![]() ,得x=﹣1或x=4,即点D的横坐标为4,∴S△ADE=S△AEH+S△DEH=
,得x=﹣1或x=4,即点D的横坐标为4,∴S△ADE=S△AEH+S△DEH=![]() (﹣ax2+3ax+4a)=﹣
(﹣ax2+3ax+4a)=﹣![]() a(x﹣
a(x﹣![]() )2+
)2+![]() a,∴△ADE的面积的最大值为
a,∴△ADE的面积的最大值为![]() a,∴
a,∴![]() a=
a=![]() ,解得:a=
,解得:a=![]() ,∴抛物线的函数表达式为y=
,∴抛物线的函数表达式为y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】三峡水库在正常运用情况下,为满足兴利除害的要求而蓄到的最高蓄水位为![]() 米,每年汛期允许蓄水的最大水位为
米,每年汛期允许蓄水的最大水位为![]() 米。在每年汛期,保证上游水位在
米。在每年汛期,保证上游水位在![]() 米的防洪限制水位,多出
米的防洪限制水位,多出![]() 米的相应库容以迎接洪峰。洪峰后,超过
米的相应库容以迎接洪峰。洪峰后,超过![]() 米的水量下泄,为下次洪峰做准备,下泄的水使中下游江面的水位升高,但不影响人们的生命和财产安全。监测水位变化的数据为防洪抗旱提供重要依据,根据多年统计,洪峰到达时万州监测点的平均水位为
米的水量下泄,为下次洪峰做准备,下泄的水使中下游江面的水位升高,但不影响人们的生命和财产安全。监测水位变化的数据为防洪抗旱提供重要依据,根据多年统计,洪峰到达时万州监测点的平均水位为![]() 米。下列是水位监测员小刘在汛期某一周每天同一时间统计的长江(万州监测点)水位高低的变化情况:(单位:米,用正数记水位比
米。下列是水位监测员小刘在汛期某一周每天同一时间统计的长江(万州监测点)水位高低的变化情况:(单位:米,用正数记水位比![]() 米的上升数,用负数记下降数)
米的上升数,用负数记下降数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化 |
|
|
|
|
|
|
|
(1)本周星期三万州监测点的实际水位是多少?
(2)若水位每上升![]() 米,蓄水量将增加
米,蓄水量将增加![]() 亿立方米,则根据数据显示,星期六的蓄水量比星期四的蓄水量增加了多少亿立方米?
亿立方米,则根据数据显示,星期六的蓄水量比星期四的蓄水量增加了多少亿立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
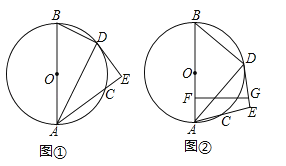
【题目】已知AB是⊙O的直径,C是圆上一点,∠BAC的平分线交⊙O于点D,过D作DE⊥AC交AC的延长线于点E,如图①.
(1)求证:DE是⊙O的切线;
(2)若AB=10,AC=6,求BD的长;
(3)如图②,若F是OA中点,FG⊥OA交直线DE于点G,若FG=![]() ,tan∠BAD=
,tan∠BAD=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)1﹣12+4
(2)﹣7﹣(﹣5)2÷(﹣1)2
(3)![]()
(4)![]()
(5)(用科学记数法表示)8.56×102﹣2.1×103
(6)用简便方法计算:﹣99![]() ×48
×48
查看答案和解析>>
科目:初中数学 来源: 题型:
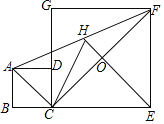
【题目】如图,正方形ABCD和正方形CEFC中,点D在CG上,BC=1,CE=3,H是AF的中点,EH与CF交于点O.
(1)求证:HC=HF.
(2)求HE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
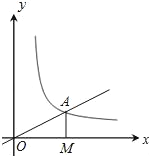
【题目】如图,正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() (k≠0)在第一象限的图象交于A点,过A点作x轴的垂线AM,垂足为M,已知△OAM的面积为1.
(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线AM,垂足为M,已知△OAM的面积为1.
(1)求反比例函数的解析式;
(2)求点A的坐标;
(3)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上确定一点P,使PA+PB最小.求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k+1)x+k2=0①有两个不相等的实数根.
(1)求k的取值范围;
(2)设方程①的两个实数根分别为x1,x2,当k=1时,求x12+x22的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C,D在线段AB上(点C,D不与线段AB的端点重合),AC+DB=![]() AB.
AB.
(1)若AB=6,请画出示意图并求线段CD的长;
(2)试问线段CD上是否存在点E,使得CE=![]() AB,请说明理由.
AB,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com