
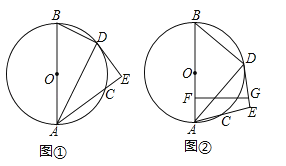
【题目】已知AB是⊙O的直径,C是圆上一点,∠BAC的平分线交⊙O于点D,过D作DE⊥AC交AC的延长线于点E,如图①.
(1)求证:DE是⊙O的切线;
(2)若AB=10,AC=6,求BD的长;
(3)如图②,若F是OA中点,FG⊥OA交直线DE于点G,若FG=![]() ,tan∠BAD=
,tan∠BAD=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() ;(3)4.
;(3)4.
【解析】试题分析:(1)欲证明DE是⊙O的切线,只要证明OD⊥DE;
(2)首先证明OD⊥BC,在Rt△BDN中,利用勾股定理计算即可;
(3)如图②中,设FG与AD交于点H,根据题意,设AB=5x,AD=4x,则AF=![]() x,想办法用x表示线段FH、GH,根据FH+GH=
x,想办法用x表示线段FH、GH,根据FH+GH=![]() ,列出方程即可解决问题;
,列出方程即可解决问题;
试题解析:解:(1)证明:如图①中,连接OD.∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠BAC,∴∠OAD=∠DAE,∴∠ODA=∠DAE,∴OD∥AE,∴∠ODE+∠AED=180°,∵∠AED=90°,∴∠ODE=90°,∴OD⊥DE,∴DE是⊙O的切线.
(2)如图①中,连接BC,交OD于点N,∵AB是直径,∴∠BCA=90°,∵OD∥AE,O是AB的中点,∴ON∥AC,且ON=![]() AC,∴∠ONB=90°,且ON=3,则BN=4,ND=2,∴BD=
AC,∴∠ONB=90°,且ON=3,则BN=4,ND=2,∴BD=![]() =
=![]() .
.
(3)如图②中,设FG与AD交于点H,根据题意,设AB=5x,AD=4x,则AF=![]() x,FH=AFtan∠BAD=
x,FH=AFtan∠BAD=![]() x
x![]() =
=![]() x,AH=
x,AH=![]() =
=![]() =
=![]() ,HD=AD﹣AH=4x﹣
,HD=AD﹣AH=4x﹣![]() =
=![]() ,由(1)可知,∠HDG+∠ODA=90°,在Rt△HFA中,∠FAH+∠FHA=90°,∵∠OAD=∠ODA,∠FHA=∠DHG,∴∠DHG=∠HDG,∴GH=GD,过点G作GM⊥HD,交HD于点M,∴MH=MD,∴HM=
,由(1)可知,∠HDG+∠ODA=90°,在Rt△HFA中,∠FAH+∠FHA=90°,∵∠OAD=∠ODA,∠FHA=∠DHG,∴∠DHG=∠HDG,∴GH=GD,过点G作GM⊥HD,交HD于点M,∴MH=MD,∴HM=![]() HD=
HD=![]() ×
×![]() =
=![]() ,∵∠FAH+∠AHF=90°,∠MHG+∠HGM=90°,∴∠FAH=∠HGM,在Rt△HGM中,HG=
,∵∠FAH+∠AHF=90°,∠MHG+∠HGM=90°,∴∠FAH=∠HGM,在Rt△HGM中,HG=![]() =
=![]() =
=![]() ,∵FH+GH=
,∵FH+GH=![]() ,∴
,∴![]() +
+![]() =
=![]() ,解得x=
,解得x=![]() ,∴此圆的半径为
,∴此圆的半径为![]() ×
×![]() =4.
=4.



 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】对于任意四个有理数![]() 、
、![]() 、
、![]() 、
、![]() ,可以组成两个有理数对
,可以组成两个有理数对![]() 与
与![]() .我们规定:
.我们规定:
![]()
![]()
![]() .
.
例如:![]()
![]()
![]() .
.
根据上述规定解决下列问题:
(1)有理数对![]()
![]()
![]() ______;
______;
(2)若有理数对![]()
![]()
![]() ,求
,求![]() 的值;
的值;
(3)当满足等式![]()
![]()
![]() 的
的![]() 是整数时,求整数
是整数时,求整数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把以下各数分别填入相应的集合里.3.14、0.121121112…、(﹣1![]() )2、|﹣6|、﹣2011、﹣22、
)2、|﹣6|、﹣2011、﹣22、![]() π、0、20%
π、0、20%
无理数集合:{ …}
负整数集合:{ …}
分数集合:{ …}
正数集合:{ …}
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
1×2=![]() (1×2×3﹣0×1×2)
(1×2×3﹣0×1×2)
2×3=![]() (2×3×4﹣1×2×3)
(2×3×4﹣1×2×3)
3×4=![]() (3×4×5﹣2×3×4)
(3×4×5﹣2×3×4)
由以上三个等式相加,可得:1×2+2×3+3×4=![]() ×3×4×5=20,读完以上材料,请你计算下列各题:
×3×4×5=20,读完以上材料,请你计算下列各题:
(1)1×2+2×3+3×4+…+10×11(写出过程)
(2)1×2+2×3+3×4+…+n×(n+1)= ;
(3)1×2×3+2×3×4+3×4×5+…+9×10×11= .
查看答案和解析>>
科目:初中数学 来源: 题型:
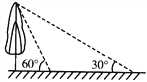
【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
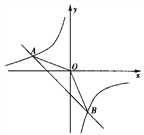
【题目】如图,一次函数![]() 的图象与反比例
的图象与反比例![]() 的图象相交于A(-2,1),B(
的图象相交于A(-2,1),B(![]() ,-2)两点.
,-2)两点.
(1)求反比例函数和一次函数的解析式;
(2) 求△ABO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
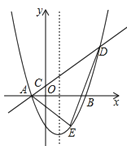
【题目】如图,在平面直角坐标系中,抛物线y=ax2-2ax-3a(a>0)与x轴交于A,B两点(点A在点B左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)求点A的坐标及直线l的函数表达式(其中k,b用含a的式子表示);
(2)点E为直线l下方抛物线上一点,当△ADE的面积的最大值为![]() 时,求抛物线的函数表达式.
时,求抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在对某二次三项式进行因式分解时,甲同学因为看错了一次项系数而将其分解为![]() ,乙同学因为看错了常数项而将其分解为
,乙同学因为看错了常数项而将其分解为![]() ,请写出正确的因式分解的结果__________
,请写出正确的因式分解的结果__________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com