
ЎѕМвДїЎїИэПїЛ®ївФЪХэіЈФЛУГЗйїцПВЈ¬ОЄВъЧгРЛАыіэє¦µДТЄЗу¶шРоµЅµДЧоёЯРоЛ®О»ОЄ![]() ГЧЈ¬ГїДкСґЖЪФКРнРоЛ®µДЧоґуЛ®О»ОЄ
ГЧЈ¬ГїДкСґЖЪФКРнРоЛ®µДЧоґуЛ®О»ОЄ![]() ГЧЎЈФЪГїДкСґЖЪЈ¬±ЈЦ¤ЙПУОЛ®О»ФЪ
ГЧЎЈФЪГїДкСґЖЪЈ¬±ЈЦ¤ЙПУОЛ®О»ФЪ![]() ГЧµД·АєйПЮЦЖЛ®О»Ј¬¶аіц
ГЧµД·АєйПЮЦЖЛ®О»Ј¬¶аіц![]() ГЧµДПаУ¦ївИЭТФУЅУєй·еЎЈєй·еєуЈ¬і¬№э
ГЧµДПаУ¦ївИЭТФУЅУєй·еЎЈєй·еєуЈ¬і¬№э![]() ГЧµДЛ®БїПВР№Ј¬ОЄПВґОєй·еЧцЧј±ёЈ¬ПВР№µДЛ®К№ЦРПВУОЅГжµДЛ®О»ЙэёЯЈ¬µ«І»У°ПмИЛГЗµДЙъГьєНІЖІъ°ІИ«ЎЈјаІвЛ®О»±д»ЇµДКэѕЭОЄ·Аєйї№єµМṩЦШТЄТАѕЭЈ¬ёщѕЭ¶аДкНіјЖЈ¬єй·еµЅґпК±НтЦЭјаІвµгµДЖЅѕщЛ®О»ОЄ
ГЧµДЛ®БїПВР№Ј¬ОЄПВґОєй·еЧцЧј±ёЈ¬ПВР№µДЛ®К№ЦРПВУОЅГжµДЛ®О»ЙэёЯЈ¬µ«І»У°ПмИЛГЗµДЙъГьєНІЖІъ°ІИ«ЎЈјаІвЛ®О»±д»ЇµДКэѕЭОЄ·Аєйї№єµМṩЦШТЄТАѕЭЈ¬ёщѕЭ¶аДкНіјЖЈ¬єй·еµЅґпК±НтЦЭјаІвµгµДЖЅѕщЛ®О»ОЄ![]() ГЧЎЈПВБРКЗЛ®О»јаІвФ±РЎБхФЪСґЖЪДіТ»ЦЬГїМмН¬Т»К±јдНіјЖµДі¤ЅЈЁНтЦЭјаІвµгЈ©Л®О»ёЯµНµД±д»ЇЗйїцЈєЈЁµҐО»ЈєГЧЈ¬УГХэКэјЗЛ®О»±И
ГЧЎЈПВБРКЗЛ®О»јаІвФ±РЎБхФЪСґЖЪДіТ»ЦЬГїМмН¬Т»К±јдНіјЖµДі¤ЅЈЁНтЦЭјаІвµгЈ©Л®О»ёЯµНµД±д»ЇЗйїцЈєЈЁµҐО»ЈєГЧЈ¬УГХэКэјЗЛ®О»±И![]() ГЧµДЙПЙэКэЈ¬УГёєКэјЗПВЅµКэЈ©
ГЧµДЙПЙэКэЈ¬УГёєКэјЗПВЅµКэЈ©
РЗЖЪ | Т» | ¶ю | Иэ | ЛД | Ое | Бщ | ИХ |
Л®О»±д»Ї |
|
|
|
|
|
|
|
ЈЁ1Ј©±ѕЦЬРЗЖЪИэНтЦЭјаІвµгµДКµјКЛ®О»КЗ¶аЙЩЈї
ЈЁ2Ј©ИфЛ®О»ГїЙПЙэ![]() ГЧЈ¬РоЛ®БїЅ«ФцјУ
ГЧЈ¬РоЛ®БїЅ«ФцјУ![]() ТЪБў·ЅГЧЈ¬ФтёщѕЭКэѕЭПФКѕЈ¬РЗЖЪБщµДРоЛ®Бї±ИРЗЖЪЛДµДРоЛ®БїФцјУБЛ¶аЙЩТЪБў·ЅГЧЈї
ТЪБў·ЅГЧЈ¬ФтёщѕЭКэѕЭПФКѕЈ¬РЗЖЪБщµДРоЛ®Бї±ИРЗЖЪЛДµДРоЛ®БїФцјУБЛ¶аЙЩТЪБў·ЅГЧЈї
Ўѕґр°ёЎїЈЁ1Ј©148.98ГЧЈ»ЈЁ2Ј©24.84ТЪБў·ЅГЧ
ЎѕЅвОцЎї
ЈЁ1Ј©УЙМвТвУГХэКэјЗЛ®О»±И![]() ГЧµДЙПЙэКэЈ¬УГёєКэјЗПВЅµКэЈ¬јхИҐРЗЖЪИэµД
ГЧµДЙПЙэКэЈ¬УГёєКэјЗПВЅµКэЈ¬јхИҐРЗЖЪИэµД![]() јґїЙЈ»
јґїЙЈ»
ЈЁ2Ј©ёщѕЭМвТв·Ц±рЗуіцРЗЖЪБщµДРоЛ®БїєНРЗЖЪЛДµДРоЛ®БїЈ¬ФЩјЖЛгЖдФцјУБїјґїЙ.
ЅвЈєЈЁ1Ј©УЙМвТвїЙµГЈє
РЗЖЪИэНтЦЭјаІвµгµДКµјКЛ®О»ОЄ![]() ЈЁГЧЈ©
ЈЁГЧЈ©
ЈЁ2Ј©ёщѕЭКэѕЭПФКѕЈ¬РЗЖЪБщµДЛ®О»ОЄ![]() ЈЁГЧЈ©
ЈЁГЧЈ©
РЗЖЪЛДµДЛ®О»ОЄ![]() ЈЁГЧЈ©
ЈЁГЧЈ©
![]() ЈЁТЪБў·ЅГЧЈ©
ЈЁТЪБў·ЅГЧЈ©
![]() РЗЖЪБщ±ИРЗЖЪЛДРоЛ®БїФцјУБЛ
РЗЖЪБщ±ИРЗЖЪЛДРоЛ®БїФцјУБЛ![]() ТЪБў·ЅГЧ.
ТЪБў·ЅГЧ.



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї¶ФУЪ·ґ±ИАэєЇКэ![]() Ј¬ПВБРЛµ·ЁІ»ХэИ·µДКЗЈЁ Ј©
Ј¬ПВБРЛµ·ЁІ»ХэИ·µДКЗЈЁ Ј©
A. µгЈЁ-2Ј¬-1Ј©ФЪЛьµДНјПсЙП B. ЛьµДНјПсФЪµЪТ»ЎўИэПуПЮ
C. µ±![]() К±Ј¬yЛжxµДФцґу¶шФцґу D. µ±
К±Ј¬yЛжxµДФцґу¶шФцґу D. µ±![]() К±Ј¬yЛжxµДФцґу¶шјхРЎ
К±Ј¬yЛжxµДФцґу¶шјхРЎ
Ўѕґр°ёЎїC
ЎѕЅвОцЎїКФМв·ЦОцЈє·ґ±ИАэєЇКэ![]() µДРФЦКЈєµ±
µДРФЦКЈєµ±![]() К±Ј¬НјПуФЪТ»ЎўИэПуПЮЈ¬ФЪГїТ»ПуПЮЈ¬yЛжxµДФцґу¶шјхРЎЈ»µ±
К±Ј¬НјПуФЪТ»ЎўИэПуПЮЈ¬ФЪГїТ»ПуПЮЈ¬yЛжxµДФцґу¶шјхРЎЈ»µ±![]() К±Ј¬НјПуФЪ¶юЎўЛДПуПЮЈ¬ФЪГїТ»ПуПЮЈ¬yЛжxµДФцґу¶шФцґу.
К±Ј¬НјПуФЪ¶юЎўЛДПуПЮЈ¬ФЪГїТ»ПуПЮЈ¬yЛжxµДФцґу¶шФцґу.
AЈ®µг![]() ФЪЛьµДНјПуЙПЈ¬BЈ®ЛьµДНјПуФЪµЪТ»ЎўИэПуПЮЈ¬CЈ®µ±
ФЪЛьµДНјПуЙПЈ¬BЈ®ЛьµДНјПуФЪµЪТ»ЎўИэПуПЮЈ¬CЈ®µ±![]() К±Ј¬
К±Ј¬![]() Лж
Лж![]() µДФцґу¶шјхРЎЈ¬ѕщХэИ·Ј¬І»·ыєПМвТвЈ»
µДФцґу¶шјхРЎЈ¬ѕщХэИ·Ј¬І»·ыєПМвТвЈ»
DЈ®µ±![]() К±Ј¬
К±Ј¬![]() Лж
Лж![]() µДФцґу¶шјхРЎЈ¬№КґнО󣬱ѕСЎПо·ыєПМвТв.
µДФцґу¶шјхРЎЈ¬№КґнО󣬱ѕСЎПо·ыєПМвТв.
їјµгЈє·ґ±ИАэєЇКэµДРФЦК
µгЖАЈє±ѕМвКфУЪ»щґЎУ¦УГМвЈ¬Ц»РиС§ЙъКмБ·ХЖОХ·ґ±ИАэєЇКэµДРФЦКЈ¬јґїЙНкіЙ.
ЎѕМвРНЎїµҐСЎМв
ЎѕЅбКшЎї
8
ЎѕМвДїЎїУЙУЪёчµШОнцІМмЖшФЅАґФЅСПЦШЈ¬2018ДкґєЅЪЗ°П¦Ј¬°ІЗмКРХюё®єЕХЩКРГсЈ¬Ѕы·ЕСМ»ЁЕЪЦс.ѧУПт3000ГыС§Йъ·ўіцЎ°јхЙЩїХЖшОЫИѕЈ¬ЙЩ·ЕСМ»Ё±¬ЦсЎ±і«ТйКйЈ¬ІўО§ИЖЎ°AАаЈєІ»·ЕСМ»Ё±¬ЦсЈ»BАаЈєЙЩ·ЕСМ»Ё±¬ЦсЈ»CАаЈєК№УГµзЧУ±ЮЕЪЈ»DАаЈєІ»»бјхЙЩСМ»Ё±¬ЦсКэБїЎ±ЛДёцСЎПоЅшРРОКѕнµчІй(µҐСЎ)Ј¬ІўЅ«¶Ф100ГыС§ЙъµДµчІйЅб№ы»жЦЖіЙНіјЖНј(ИзНјЛщКѕ).ёщѕЭійСщЅб№ыЈ¬Зл№АјЖИ«РЈЎ°К№УГµзЧУ±ЮЕЪЎ±µДС§ЙъУРЈЁ Ј©
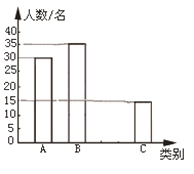
A. 900Гы B. 1050Гы C. 600Гы D. 450Гы
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї¶ФУЪИОТвЛДёцУРАнКэ![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() Ј¬їЙТФЧйіЙБЅёцУРАнКэ¶Ф
Ј¬їЙТФЧйіЙБЅёцУРАнКэ¶Ф![]() Ул
Ул![]() .ОТГЗ№ж¶ЁЈє
.ОТГЗ№ж¶ЁЈє
![]()
![]()
![]() .
.
АэИзЈє![]()
![]()
![]() .
.
ёщѕЭЙПКц№ж¶ЁЅвѕцПВБРОКМвЈє
ЈЁ1Ј©УРАнКэ¶Ф![]()
![]()
![]() ______Ј»
______Ј»
ЈЁ2Ј©ИфУРАнКэ¶Ф![]()
![]()
![]() Ј¬Зу
Ј¬Зу![]() µДЦµЈ»
µДЦµЈ»
ЈЁ3Ј©µ±ВъЧгµИКЅ![]()
![]()
![]() µД
µД![]() КЗХыКэК±Ј¬ЗуХыКэ
КЗХыКэК±Ј¬ЗуХыКэ![]() µДЦµ.
µДЦµ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
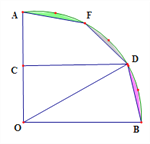
ЎѕМвДїЎїИзНјЈ¬ЙИРОЦЅЖ¬AOBЦР,ТСЦЄЎПAOB=90,OA=6Ј¬ИЎOAµДЦРµгCЈ¬№эµгCЧчDCЎНOAЅ»![]() УЪµгDЈ¬µгFКЗ
УЪµгDЈ¬µгFКЗ![]() ЙПТ»µг.ИфЅ«ЙИРОBODСШOD·ХЫЈ¬µгBЗЎєГУлµгFЦШєПЈ¬УГјфµ¶СШЧЕПЯ¶ОBDЎўDFЎўFAТАґОјфПВЈ¬ФтКЈПВµДЦЅЖ¬ЈЁТхУ°Ії·ЦЈ©Гж»эКЗ______________.
ЙПТ»µг.ИфЅ«ЙИРОBODСШOD·ХЫЈ¬µгBЗЎєГУлµгFЦШєПЈ¬УГјфµ¶СШЧЕПЯ¶ОBDЎўDFЎўFAТАґОјфПВЈ¬ФтКЈПВµДЦЅЖ¬ЈЁТхУ°Ії·ЦЈ©Гж»эКЗ______________.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
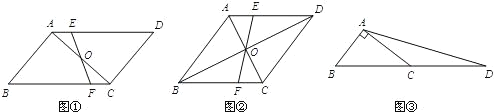
ЎѕМвДїЎї(1)ІВПлЈєИзНјўЩЈ¬ФЪ![]() ЦРЈ¬µг
ЦРЈ¬µг![]() КЗ¶ФЅЗПЯ
КЗ¶ФЅЗПЯ![]() µДЦРµгЈ¬№эµг
µДЦРµгЈ¬№эµг![]() µДЦ±ПЯ·Ц±рЅ»
µДЦ±ПЯ·Ц±рЅ»![]() Ўў
Ўў![]() УЪµг
УЪµг![]() Ўў
Ўў![]() Ј¬Иф
Ј¬Иф![]() µДГж»эКЗ8Ј¬ФтЛД±ЯРО
µДГж»эКЗ8Ј¬ФтЛД±ЯРО![]() µДГж»эКЗ________.
µДГж»эКЗ________.
(2)МЅѕїЈєИзНјўЪЈ¬ФЪБвРО![]() ЦРЈ¬¶ФЅЗПЯ
ЦРЈ¬¶ФЅЗПЯ![]() Ўў
Ўў![]() Ѕ»УЪµг
Ѕ»УЪµг![]() Ј¬№эµг
Ј¬№эµг![]() µДЦ±ПЯ·Ц±рЅ»
µДЦ±ПЯ·Ц±рЅ»![]() Ўў
Ўў![]() УЪµг
УЪµг![]() Ўў
Ўў![]() Ј¬Иф
Ј¬Иф![]() Ј¬
Ј¬![]() Ј¬ЗуЛД±ЯРО
Ј¬ЗуЛД±ЯРО![]() µДГж»э.
µДГж»э.
(3)У¦УГЈєИзНјўЫЈ¬ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬СУі¤
Ј¬СУі¤![]() µЅµг
µЅµг![]() Ј¬К№
Ј¬К№![]() Ј¬Б¬Ѕб
Ј¬Б¬Ѕб![]() Ј¬Иф
Ј¬Иф![]() Ј¬
Ј¬![]() Ј¬Фт
Ј¬Фт![]() µДГж»эКЗ_______.
µДГж»эКЗ_______.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИф№ШУЪxµД·ЅіМ-2x+m![]() +4020=0ґжФЪХыКэЅвЈ¬ФтХэХыКэmµДЛщУРИЎЦµµДєНОЄ___________.
+4020=0ґжФЪХыКэЅвЈ¬ФтХэХыКэmµДЛщУРИЎЦµµДєНОЄ___________.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї°СТФПВёчКэ·Ц±рМоИлПаУ¦µДјЇєПАпЈ®3.14Ўў0.121121112ЎЎўЈЁ©Ѓ1![]() Ј©2Ўў|©Ѓ6|Ўў©Ѓ2011Ўў©Ѓ22Ўў
Ј©2Ўў|©Ѓ6|Ўў©Ѓ2011Ўў©Ѓ22Ўў![]() ¦РЎў0Ўў20%
¦РЎў0Ўў20%
ОЮАнКэјЇєПЈє{ЎЎ ЎЎЎ}
ёєХыКэјЇєПЈє{ЎЎ ЎЎЎ}
·ЦКэјЇєПЈє{ЎЎ ЎЎЎ}
ХэКэјЇєПЈє{ЎЎ ЎЎЎ}
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФД¶БПВБРІДБПЈє
1ЎБ2ЈЅ![]() ЈЁ1ЎБ2ЎБ3©Ѓ0ЎБ1ЎБ2Ј©
ЈЁ1ЎБ2ЎБ3©Ѓ0ЎБ1ЎБ2Ј©
2ЎБ3ЈЅ![]() ЈЁ2ЎБ3ЎБ4©Ѓ1ЎБ2ЎБ3Ј©
ЈЁ2ЎБ3ЎБ4©Ѓ1ЎБ2ЎБ3Ј©
3ЎБ4ЈЅ![]() ЈЁ3ЎБ4ЎБ5©Ѓ2ЎБ3ЎБ4Ј©
ЈЁ3ЎБ4ЎБ5©Ѓ2ЎБ3ЎБ4Ј©
УЙТФЙПИэёцµИКЅПајУЈ¬їЙµГЈє1ЎБ2+2ЎБ3+3ЎБ4ЈЅ![]() ЎБ3ЎБ4ЎБ5ЈЅ20Ј¬¶БНкТФЙПІДБПЈ¬ЗлДгјЖЛгПВБРёчМвЈє
ЎБ3ЎБ4ЎБ5ЈЅ20Ј¬¶БНкТФЙПІДБПЈ¬ЗлДгјЖЛгПВБРёчМвЈє
ЈЁ1Ј©1ЎБ2+2ЎБ3+3ЎБ4+Ў+10ЎБ11ЈЁРґіц№эіМЈ©
ЈЁ2Ј©1ЎБ2+2ЎБ3+3ЎБ4+Ў+nЎБЈЁn+1Ј©ЈЅЎЎЎЎЈ»
ЈЁ3Ј©1ЎБ2ЎБ3+2ЎБ3ЎБ4+3ЎБ4ЎБ5+Ў+9ЎБ10ЎБ11ЈЅЎЎЎЎЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
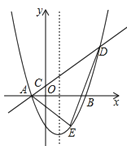
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬ЕЧОпПЯyЈЅax2Ј2axЈ3aЈЁaЈѕ0Ј©УлxЦбЅ»УЪAЈ¬BБЅµгЈЁµгAФЪµгBЧуІаЈ©Ј¬ѕ№эµгAµДЦ±ПЯlЈєyЈЅkxЈ«bУлyЦбЅ»УЪµгCЈ¬УлЕЧОпПЯµДБнТ»ёцЅ»µгОЄDЈ¬ЗТCDЈЅ4ACЈ®
ЈЁ1Ј©ЗуµгAµДЧш±кј°Ц±ПЯlµДєЇКэ±нґпКЅЈЁЖдЦРkЈ¬bУГє¬aµДКЅЧУ±нКѕЈ©Ј»
ЈЁ2Ј©µгEОЄЦ±ПЯlПВ·ЅЕЧОпПЯЙПТ»µгЈ¬µ±ЎчADEµДГж»эµДЧоґуЦµОЄ![]() К±Ј¬ЗуЕЧОпПЯµДєЇКэ±нґпКЅЈ®
К±Ј¬ЗуЕЧОпПЯµДєЇКэ±нґпКЅЈ®
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com